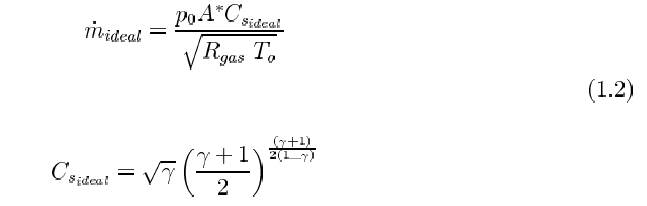・Discharge Coefficientの計算
イスラエルはBen-Gurion大学と行っている共同研究で持ち上がった疑問.「Phoenicsは,圧縮性,粘性流体のDischarge
coefficientをきちんと計算できるのか?」これを確認するために行った計算.一種のベンチマークかな?
Duscharge coefficientとは以下のようなものである.
圧縮性流体をオリフィスから噴出させるときの質量流量は,オリフィスにおけるマッハ数が1に決まってしまうため以下の数式で計算できる.
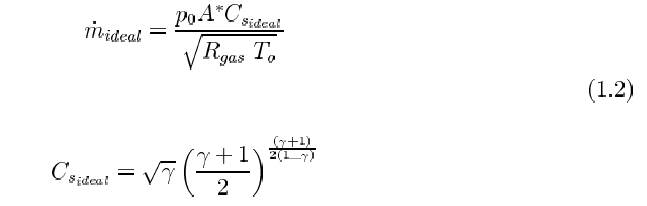
ところが,この式には流体の粘性の効果が入っていない.粘性流体の場合,プレナムの圧力が低くなると,言い換えればガスの粘性力が慣性力に比べて無視できなくなると,質量流量は(1)式の値より小さくなる.この比率

をDischarge coefficientと言い,詳しい解析によるとこれはオリフィスのReynolds
numberの逆数の1/2乗に比例することが知られている.
図3は,ISO9300標準ノズル(図4)において,Discharge coefficientがReの関数でどのように変化するかを実験により確かめたものである.
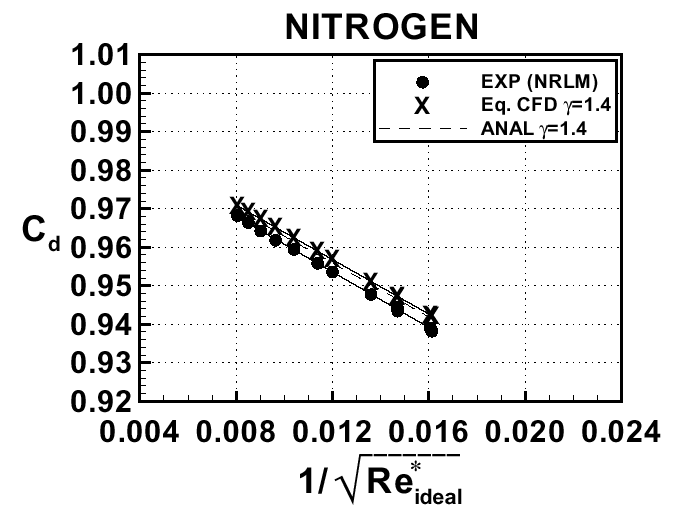
図3:窒素ノズルにおける,レイノルズ数とCdの関係(下記参考文献p80より転載)

図4: ISO9300標準ノズル
これが,Phoenicsで再現するかどうかチェックしてみた.
上の説明で用いた図は全てhttp://www.cstl.nist.gov/div836/836.01/PDFs/2000/Aaron_dissertation.pdfから転載した.
計算1: 円筒対称二次元,細かいメッシュ
まずは,解析解となるべく近い値が出るように,細かいメッシュで計算してみた.形は円筒対象なので,当然円筒座標系を採用.
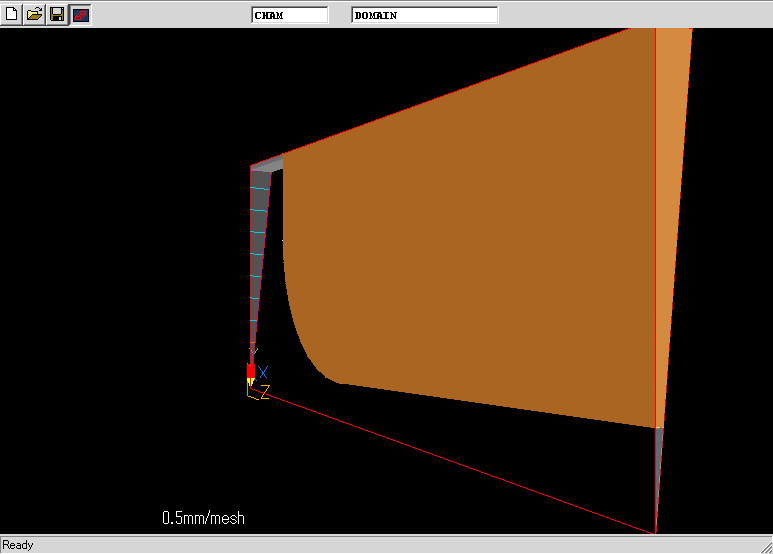

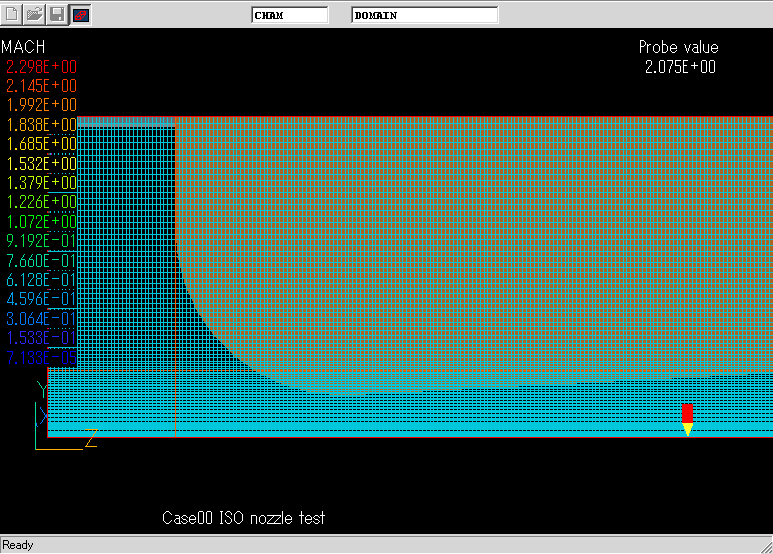
計算結果の一例
###############################################################################
## Case13 ########################################################### 03/06/12#
###############################################################################
##Domain and Variables
## Title: Case13<-09 Sutherland viscosity m=1/2
## Mesh number x= 1 y=100 z=200
## Domain size 0.1 [rad]
## 5×12 [mm]
## Mass flow: 1.64e-005 [kg/s]
## Tubulence model OFF
## Outlet pressure 500.0 [Pa] coeff. 1
##
## Calculation options:
## EXPERT = ON
## DENPCO = ON
## WFIELD = P1 , V1 , W1 , TEM1,
## SOLVE = SOLVE(P1 ,V1 ,W1 ,TEM1)
## STORE = STORE(PRPS,DEN1,MACH)
##
## Calculation convergence
## variable resref (res sum)/resref
## P1 3.446E-12 1.146E+02
## V1 4.176E-11 1.587E+02
## W1 7.867E-10 1.071E+01
## TEM1 9.155E-07 1.165E+00
## Discharge coefficient:
## p0 = 6.058843e+003
## A* = 1.327323e-006
## T0 = 2.996823e+002
## m = 1.642425e-005
## m_ideal = 1.845948e-005
## Re_ideal = 1.010028e+003
## 1/(Re_ideal)^(1/2) = 3.146541e-002
## Cd = 8.897457e-001
## Cd(NACA table) = 8.838297e-001
##
q1 file
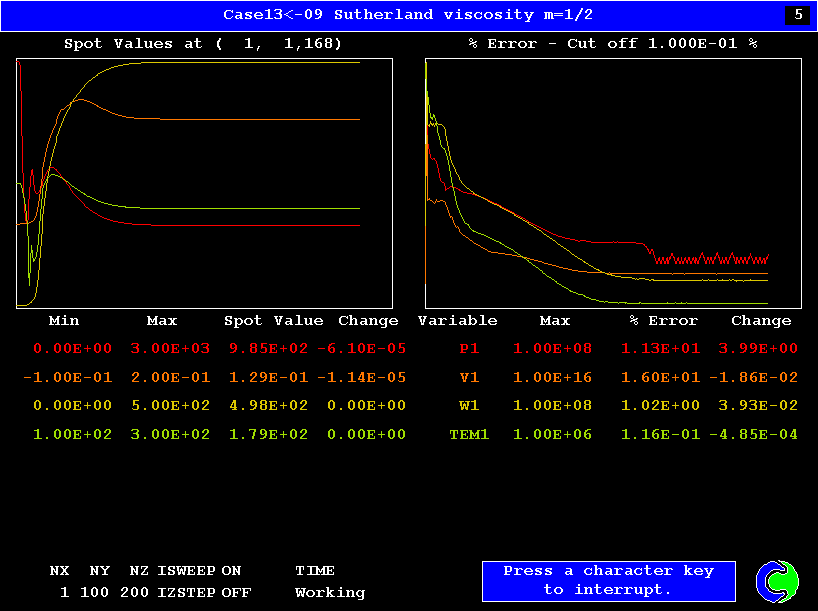
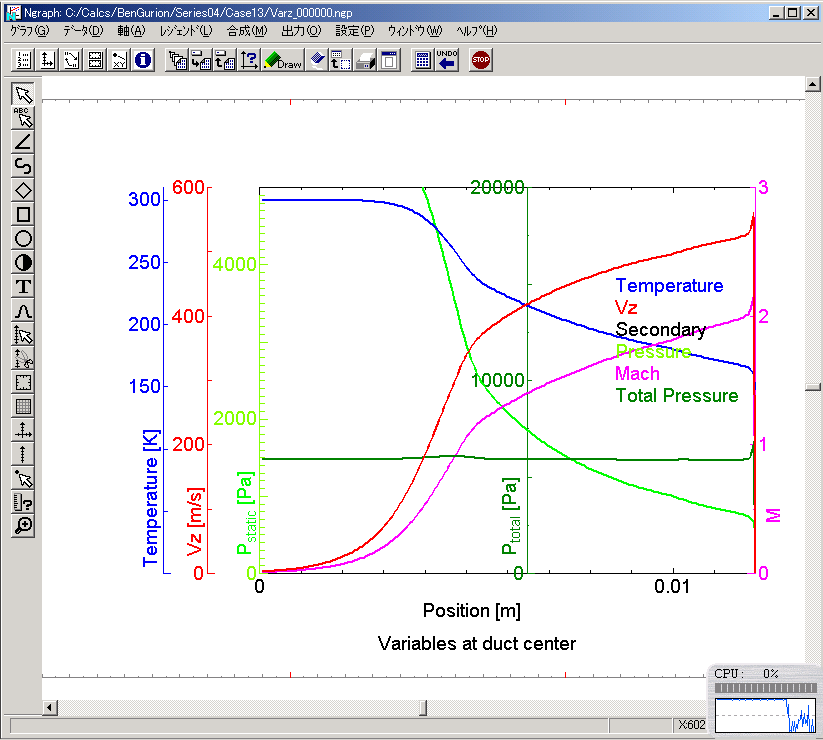
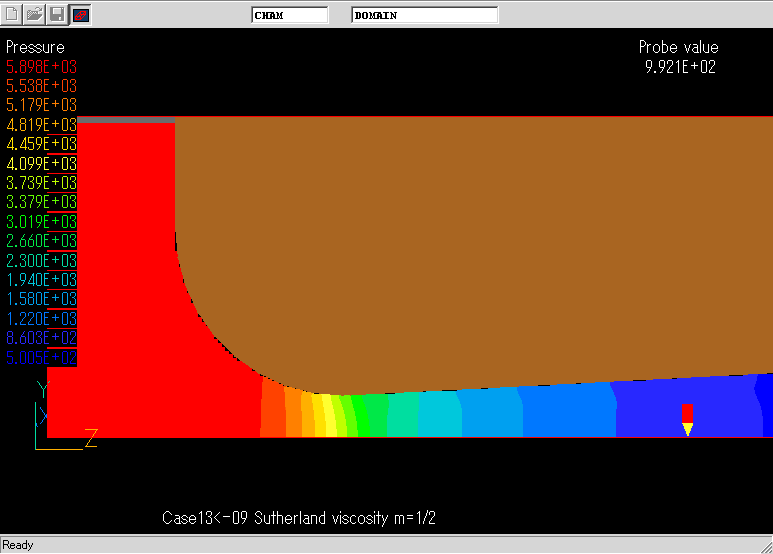
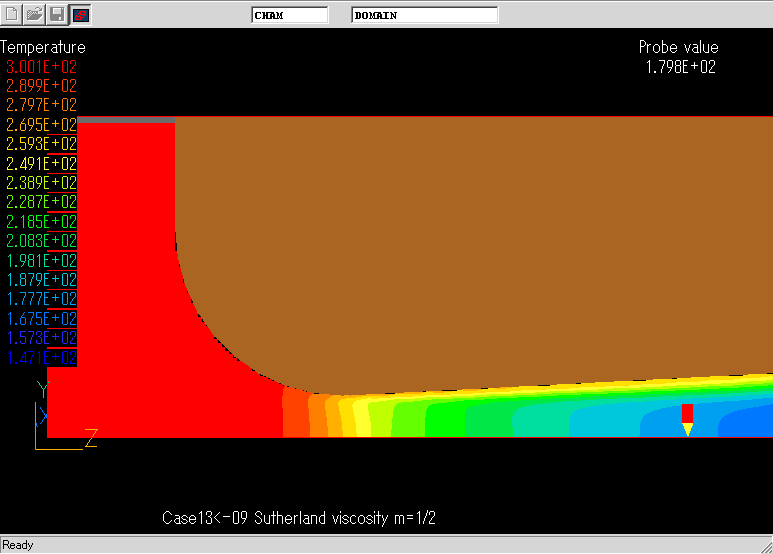
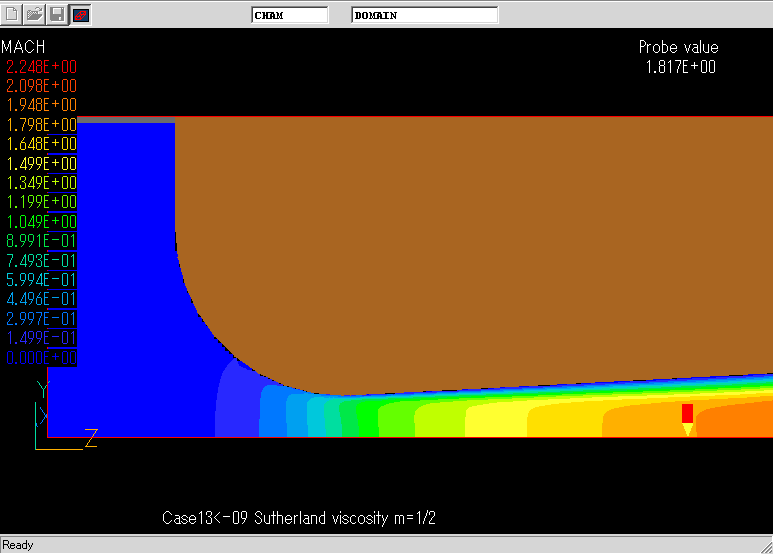
レイノルズ数とDischarge coefficientの関係.NACAによる実験結果と良く一致している.

計算2: デカルト座標三次元,粗いメッシュ
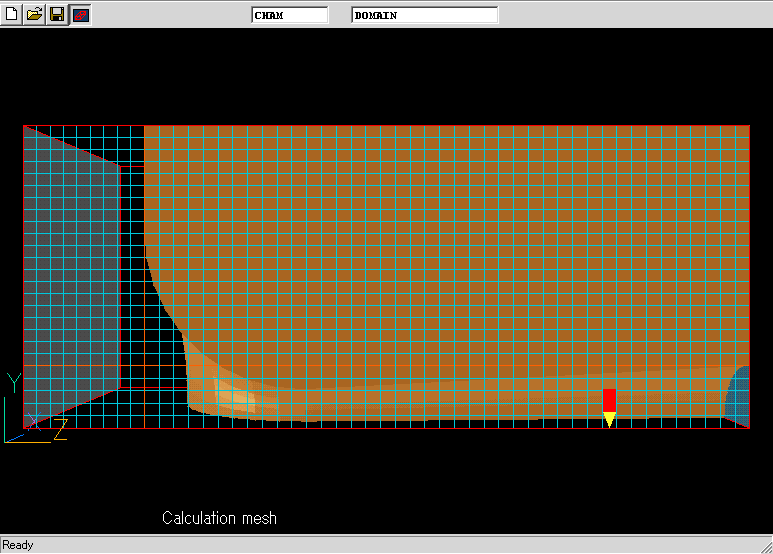
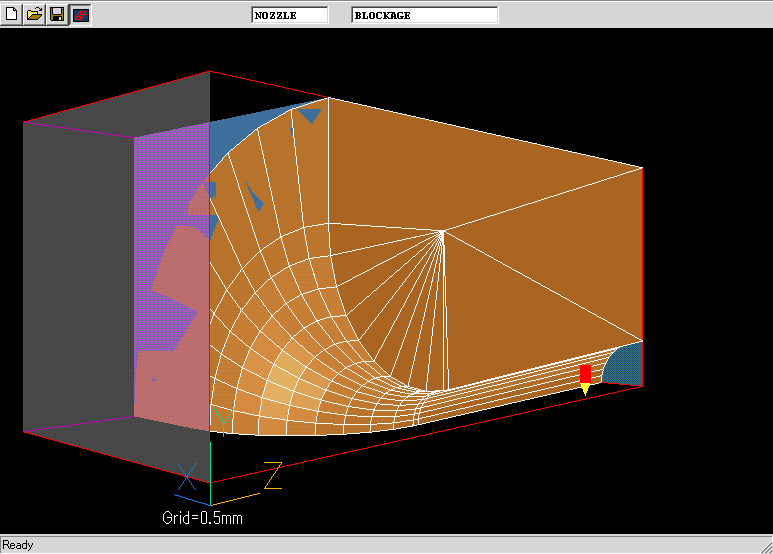
COILの計算には,計算領域に比べて非常に小さいオリフィスが存在するケースがよくある.こういう場合のメッシュ数を節約したいが,どのていどまでは行けるのか,デカルト座標であえて粗いメッシュを用い,計算を行った.デカルト座標の場合,対称性から1/4円弧部分を計算すればよい.
計算結果の一例
###############################################################################
## Case02 ########################################################### 03/06/12#
###############################################################################
##Domain and Variables
## Title: Case02 Mass flow 25.0
## Mesh number x= 25 y= 25 z= 50
## Domain size 0.005 [rad]
## 5×12 [mm]
## Mass flow: 4.59e-005 [kg/s]
## Tubulence model OFF
## Outlet pressure 1000.0 [Pa] coeff. 1
##
## Calculation options:
## EXPERT = ON
## DENPCO = ON
## WFIELD = P1 , V1 , W1 , TEM1,
## SOLVE = SOLVE(P1 ,U1 ,V1 ,W1 ,TEM1)
## STORE = STORE(PRPS,DEN1,MACH)
##
## Calculation convergence
## variable resref (res sum)/resref
## P1 2.720E-11 4.405E+01
## U1 3.360E-10 1.008E+03
## V1 3.360E-10 1.024E+03
## W1 5.428E-09 3.467E+01
## TEM1 7.153E-06 1.892E+00
## Discharge coefficient:
## p0 = 1.619838e+004
## A* = 1.327323e-006
## T0 = 2.996916e+002
## m = 4.588000e-005
## m_ideal = 4.935086e-005
## Re_ideal = 2.700278e+003
## 1/(Re_ideal)^(1/2) = 1.924402e-002
## Cd = 9.296698e-001
## Cd(NACA table) = 9.289511e-001
##
q1 file
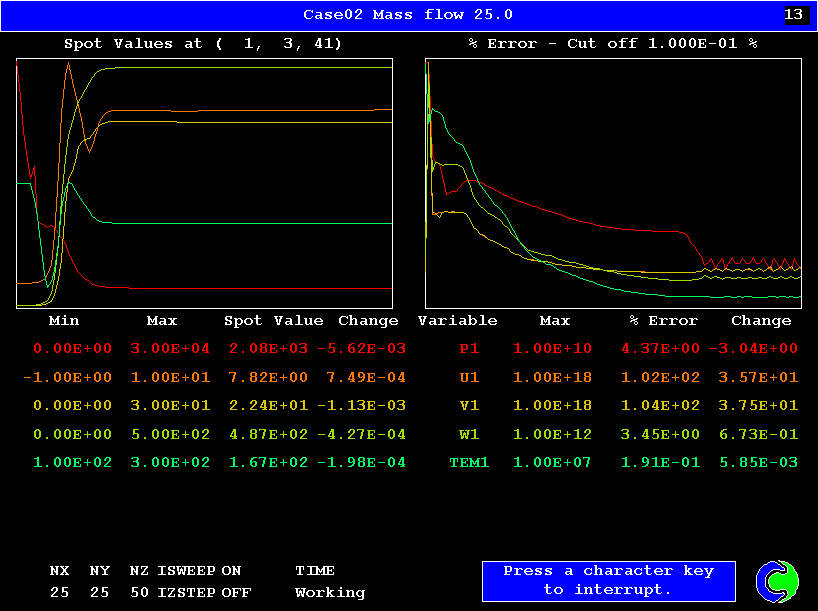
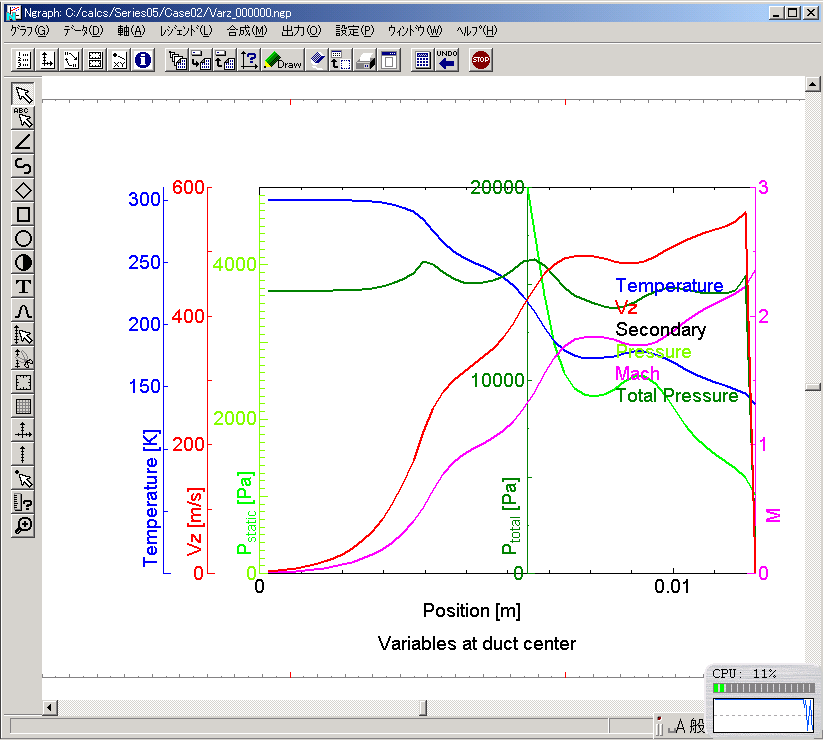
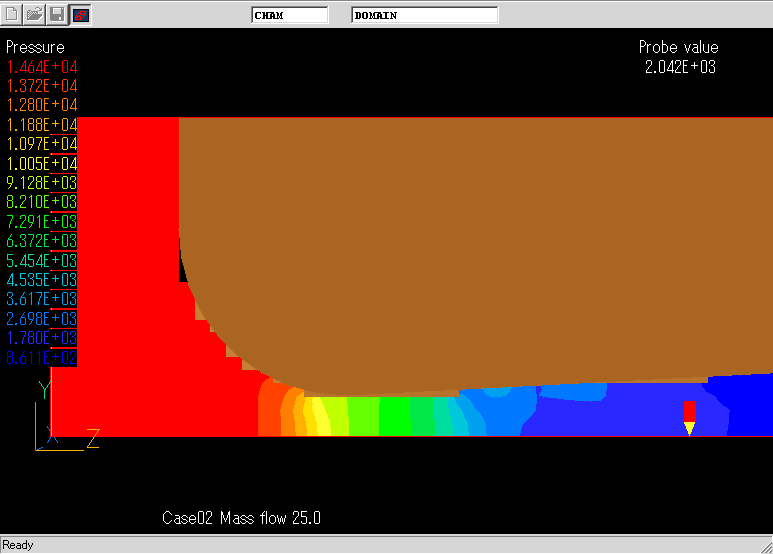
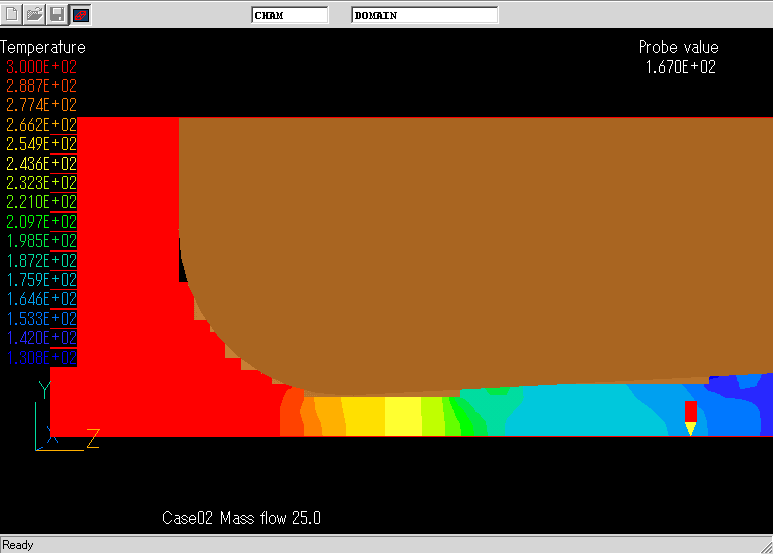
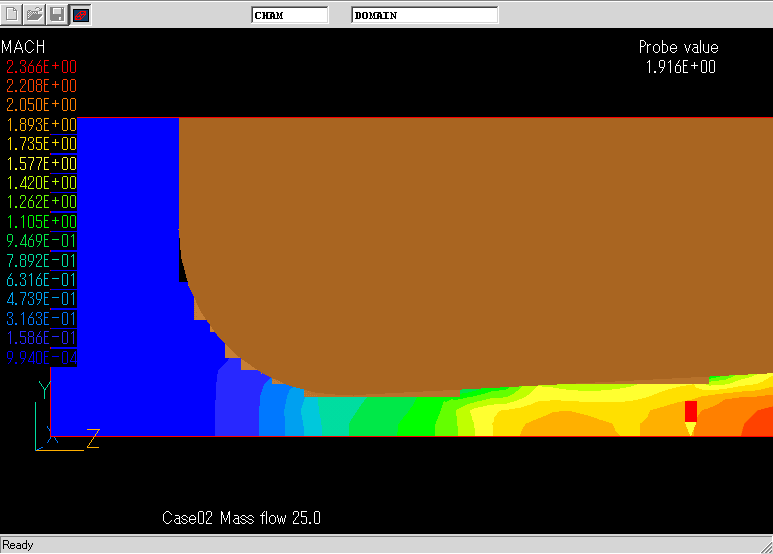
レイノルズ数とDischarge coefficientの関係.これほど,粗いメッシュにもかかわらずNACAによる実験結果と良く一致している.
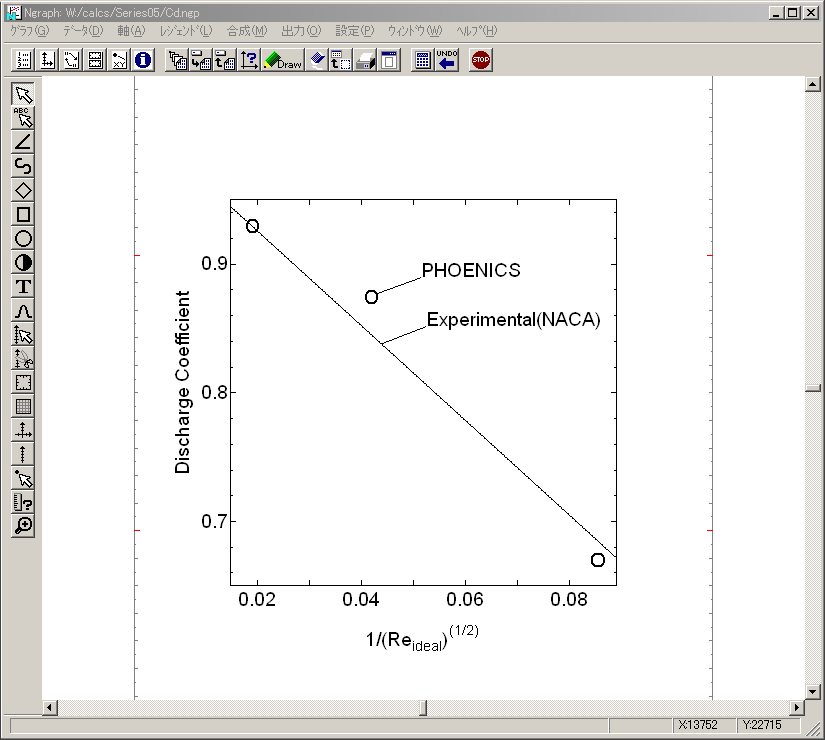
結論:Phoenicsによる圧縮性,粘性流体の計算は実験と非常に良い一致をみた.