・開放系の流出境界条件

　今回は，「開放系」の流出境界条件について考えてみよう．開放系とは，系の6面全てが流出境界となるような系である．実際には対称性から流出境界が5面で済む場合も多いと思う．具体的には本研究室で行っているレーザー切断の様な系だ．

　このような系では，領域の端は全て「流出境界」面としなければいけない．さもないと，そこには仮想のスリップ壁が置かれたのと同じ計算となってしまい，意図したとおりの結果が得られない．ここで問題になるのが境界条件だ．ダクトの流れの様な内部流れの場合，流出境界におけるおよその流速(の3成分)はわかっており，それを境界条件として与えることが出来る．しかし，開放系の場合，ガスがどの面からどれくらい流出するかはアプリオリには決定できない．それを決めるのが計算の目的の一つなのだから．

　一方，Phoenicsが流出境界において与えうるのは，面全体にわたって圧力，温度，流速などの物理量を

1. 一定の値に固定する
   
2. In-cell，つまりdφ/dx=0とする

　かのどちらかだ(In-formで複雑な流出境界を設定することもできるがそれは今回の話題とは直接は関係ない)．一見，全ての境界条件をIn-cellとすれば，系の内，外で矛盾が起こらないので好ましいように思われるがそうでもないことが以下の実験からわかる．

・今回使用したテストケース

　計算は，レーザー切断ノズルとスラブからなる系を簡略化したもの．上から流入するガスをC1でマークした．

・流出境界のバリエーション

　流出境界は，下の図のように，この計算では

• 圧力
• Coefficient
• 温度
• 乱流エネルギーと乱流エネルギー散逸率
• 流速(x，y，z)
• C1

を規定する．

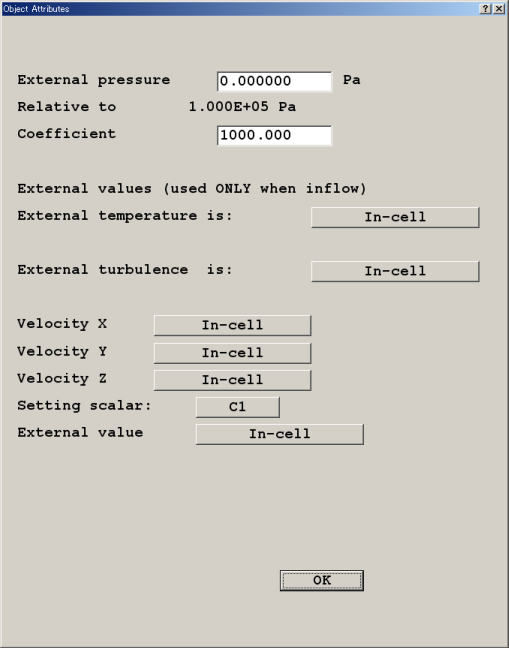
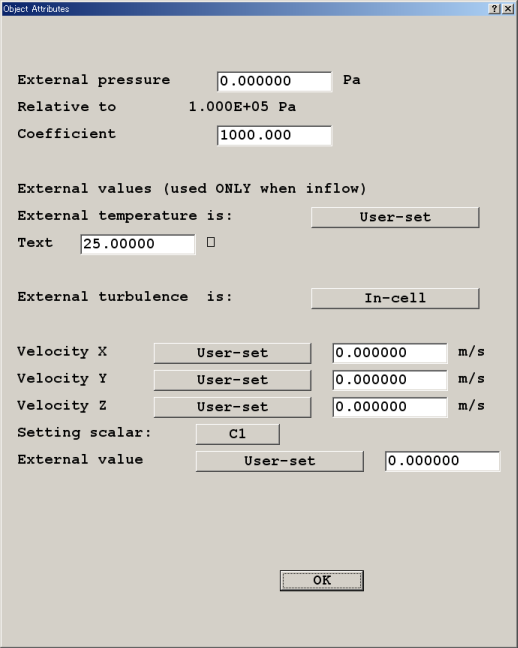
圧力だけは絶対値で指定する必要があるが，あとの物理量は「In-cell」か，具体的な数値かを選ぶことが出来る．Coefficientの意味は，マニュアルの記述を一般的な日本語に翻訳すると，「系の中の値と，系の外に規定された値が食い違うとき，どれだけ中の状態を外にあわせようとがんばるか」という係数である．Phoenicsのかつてのバージョンではこの値は1,000で固定だったそうだが，Ver. 3あたりからユーザーが規定可能な変数になったと聞く．Ooefficientについての詳しい情報はここ．

・4つの計算結果を比較

　ここで，4面の流出境界の条件が以下のように異なる4ケースの計算を行い，結果を比較する．

ここで，流出境界条件の「0」とは，圧力0，流速0，温度は常温の25℃，C1=0と規定した条件である．圧力は，Phoenicsの仕様によりIn-cellのケースでも0.0固定，乱流境界条件は全てのケースでIn-cellとした．

以下の画像は結果の比較である．全ての画像が上から順番にCase0，1，2,，3の結果を表す．

GXMONI

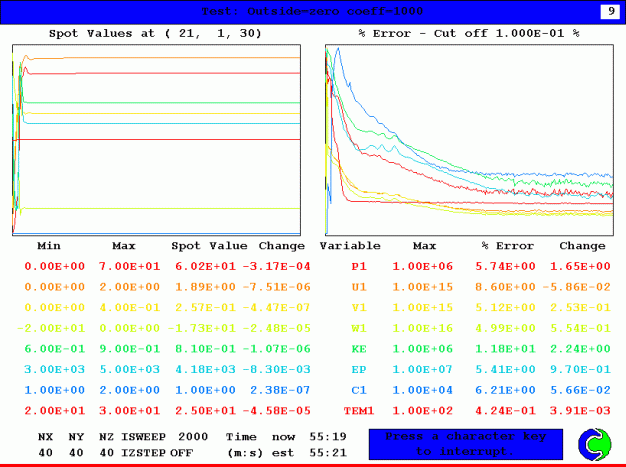
圧力

流速

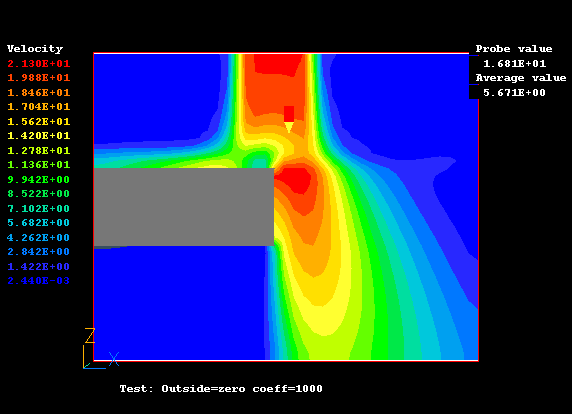
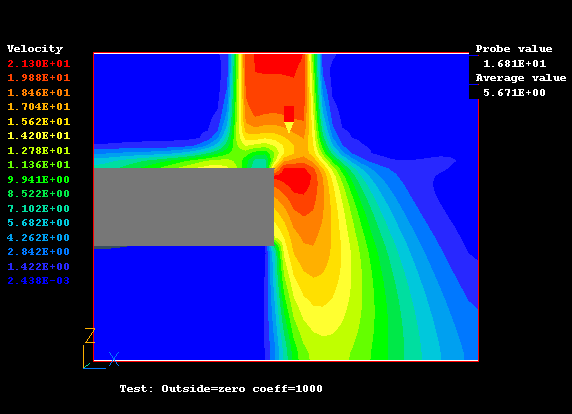
C1

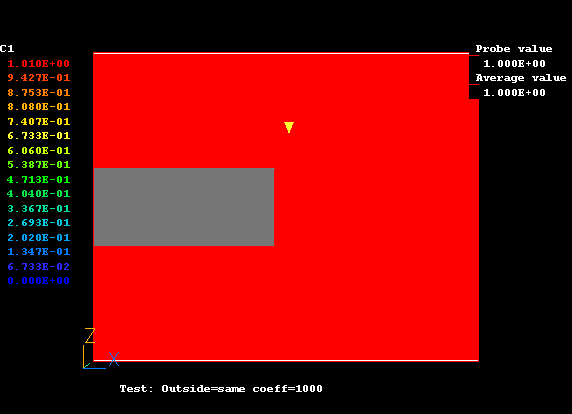
・計算結果からわかること　

1. Coefficient=1000，In-cell境界のCase0は収束に至らなかった．流速，圧力も他の三つのケースとは異なる．Case1，2，3については，流速と圧力に関しては一致をみたが，C1については0とIn-cellのケースで大きく異なる．
   
2. C1の分布は，In-cellと0とでは全く異なる．境界条件をIn-cellとしたことで，C1の行き場が無くなり，系内に充満してしまうと言うことが明らかだ．上ガスがどのような経路で系外に流れ出すかを知るのが計算の目的なので，これでは役に立たない．
   
3. 計算の収束は，Case0は論外としても，In-cellより0の方が良い．理由は，dφ/dx=0というのは系内部での物理量のの大きさを規定するわけではないので，系内部の自由度が大きく，限られたループ数で一定の収束が得られなかったものである．
   
4. Coefficientの1と1000を比べた場合は，収束は1の方が良い．特に，境界条件をIn-cellとした場合，収束には至らなかったのでその違いは顕著である．理由は，系外の物理量を一定とした境界条件は，どうがんばっても系内との不整合が発生し，coefficientが大きい場合はその不整合を無くそうと「がんばる」ので，収束が遅くなるものと思われる．最終的に収束した計算については，その圧力，流速分布には見た目でわかるような差はない．

　ここから，以下のような結論が導かれる．

・まとめ

• 開放系における，流出境界条件について考察した．その結果，開放系における境界条件は，物理量を「0」に固定し，coefficientを小さくセットするのが良いと言うことがわかった．