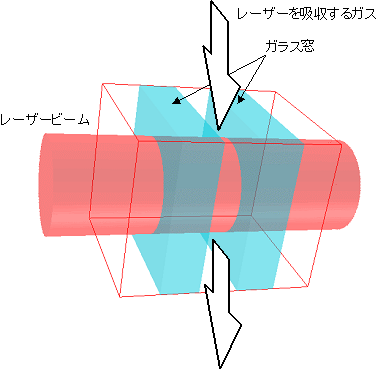
図1: 問題の提示
・レーザービームで加熱されるガスの計算(In-Form)
・まえがき

図1: 問題の提示
図1のような問題を考えよう.二枚のガラス板で挟まれた空間に,レーザービームを吸収する性質のあるガスが満たされており,冷却を助けるために循環している.ビームはガラス板に垂直に入射する.このとき,温められたガスの熱がガラスに伝わるわけだが,ガラスの温度はどのくらい上昇するだろうか.
こういう問題を依頼され,計算を始めた.「レーザービームの吸収」というところがPhoenics使いのウデの見せ所.この問題をどう解くか,三つのステップで見ていこう.
・系の定義
系はビーム軸に垂直な面について対称と考える.要するに,ガスの吸収係数は小さく,通過したビームはほとんど減衰しないと仮定するわけだ.これで計算領域が半分になる.同様に,系はビーム進行方向に対して左右にも対称なのだが,見栄えを重視してここはfull widthで解こう.簡単のため,ガラスは側面温度固定,セル表面は断熱境界とする.こうするとセル外側を考えなくても良い.ビームを吸収するのはガスだけで,ガラスは完全に透明とする.ガスの物性は,特殊なガスなら物性値を定義する必要があるが,今回は窒素ガスとしよう.セル内部の圧力は大気圧で,流入境界は流速一定,流出境界は圧力固定とする.ここまでで,VR-Viewer上で見た系の概念図は図2の様になる.

図2: 系の定義
・解法1: Domain fluidに熱ソース項を持たせる
レーザービームはTEM00のガウスビームとする.これがガスを垂直に貫くモデルを作ればよいわけだが,VR-Viewerの機能だけで完全にこれを実現することはできない.まず,誰でも思いつく簡単な方法として,ガウスビームを複数のリングで近似し,各リングに一定の熱源を与えよう.リングはDomain Fluidで定義しておけば,ガスが流れて熱源だけが空間に固定されたモデルができる.ガスが吸収する熱量を200Wと仮定しよう.系はハーフモデルなので吸熱は100W.
ビームを,スポットサイズw0の2.5倍まで取り,これを5個のゾーンに分解する.計算は少々面倒だが,Excelを使えばごらんの通り.
| 半径 | 値 | リング面積 | パワー | 相対パワー | π | 3.1416 |
| exp(-r^2) | π[r(i)^2-r(i-1)^2] | =値×面積 | 全パワーを 100Wに規格化 |
|||
| 0 | 1 | 全パワー | 100 | |||
| 0.5 | 0.778800783 | 0.7854 | 0.7854 | 16.45160342 | ||
| 1 | 0.367879441 | 2.3562 | 1.835010405 | 38.43756487 | ||
| 1.5 | 0.105399225 | 3.927 | 1.444662565 | 30.26103336 | ||
| 2 | 0.018315639 | 5.4978 | 0.579463857 | 12.1379037 | ||
| 2.5 | 0.001930454 | 7.0686 | 0.129465925 | 2.711894646 | ||
| 4.774002752 |
熱源の定義は,Attributesのタブで以下のように設定.

出来上がったq1ファイルをここに示す.計算結果は図3のとおり.ガス温度は309℃まで上昇し,ガラス表面は200℃程度まで上昇することが分かる.これによる熱レンズ効果の計算とビーム揺動の評価が仕事なのだが,ここでは語らない.


図3: 円柱近似法にて計算したガスおよびガラス窓の温度
・解法2: ガウス関数で変化する熱源をエンベッド
Phoenicsには,VR-Viewerの設定ではできないような高度な物性値,境界条件,ソース項などの設定を行うIn-Formという機能がある.メカニズムとしては
という形を取る.かつては同様のことを行うのにPhoenics自身を再コンパイルする必要があったのだが,In-Formの登場によりこれが非常に気楽にできるようになった.今回のようにちょっと難しい条件を取り扱うには実に便利な方法だ.
まず,上述のq1ファイルから熱源を定義した円柱を取り去る.そして,ガスの存在範囲一杯に「BEAMG」なるオブジェクトを定義.オブジェクト種類はUser-Definedだ.ここまでやったらq1ファイルを閉じ,エディタを使い以下の部分を追加.場所は,Group13のEGWF=Tの後ろあたり.この辺は結構アバウトで,VR-Editorが勝手に整形してくれる.なお,下には各行にコメントを入れてあるが,このままVR-Editorに入れてしまうとエラーになる.
SAVE13BEGIN // お約束 CHAR(GA,GB) // ユーザ変数定義 GA=-2*((YVLAST/2.0-YG)^2+(ZWLAST/2.0-ZG)^2)/(5.0E-3)^2 // ガウスビームの定義 GB=1.116E9*EXP(:GA:) // 単位体積当たり発熱量を掛ける (SOURCE TEM1 AT BEAMG IS DEN1*VOL*:GB:) // 各セルの発熱量を計算,TEM1のソース項とする (STORED HG AT BEAMG IS DEN1*:GB:) // 変数HGに体積当たり発熱量をストア SAVE13END // お約束
きちんと動くものはこちら.
(STORED HG...の行は無くても全く問題ないのだが,これを入れておくとVR-Viewerで発熱分布を見ることができる.
計算結果はどうなったか.図3と比べてみよう.なんと,最高温度(ΔT)が100K近く下がっている.上述の円柱近似には大きな誤差があることが明らかとなった.
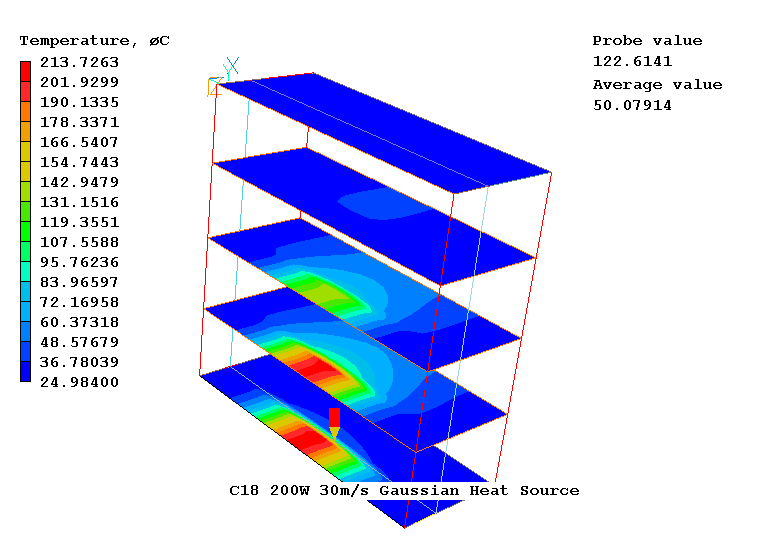

図4: In-Formを用い,ガウス発熱分布にて計算したガスおよびガラス窓の温度

図5: 発熱分布
・解法3: 吸収係数を圧力に比例させる
最後に,上のモデルでは考慮していなかったが重要な現象をモデル化する.ガスは暖まると膨張し,吸収係数はガス密度に比例する.従って,ローカルな発熱量は,ビーム強度×密度に比例するはずだ.物理的なモデルは,上のIn-FormにDEN1をかけるだけだが,この方法だと全発熱量が不定となる.ある発熱量を与えたときの温度が知りたいのだから,これでは不便.そこで,かなりトリッキーな手を使い,発熱量が100Wになるようフィードバック制御を掛ける.In-Form部分は以下のようになる.完全なq1ファイルはこちら.
SAVE13BEGIN CHAR(GA) GA=-2*((YVLAST/2.0-YG)^2+(ZWLAST/2.0-ZG)^2)/(5.0E-3)^2 (SOURCE TEM1 AT BEAMG IS H0*DEN1*VOL*EXP(:GA:)) // H0が基準熱量となる (STORED HG AT BEAMG IS H0*DEN1*EXP(:GA:)) (STORED HE AT BEAMG IS H0*DEN1*VOL*EXP(:GA:)) (STORED H1 AT BEAMG IS SUM(HE)) // 今回のループの全発熱量を計算,HEにストア (STORED H0 AT BEAMG IS H0*((100.0-H1)/100.0+1.0)) // HE=100WになるようH0を調整 SAVE13END
計算結果は以下の通り.解法2と比べて,ガス密度の最も低い部分は常温の半分しかないため吸収率も半分のはずだが,温度分布はそれほど大きくは変わっていない.理由は,全発熱量を同じとして計算したことと,発熱は結局流れるガスにより積分されるため,温度上昇は変わらないためと思われる.


図6: In-Formとフィードバック制御を用い,密度に比例する発熱分布にて計算したガスおよびガラス窓の温度
発熱分布は,暖まったガスが下側に流れる結果密度が下がる影響を受けて上方にシフトしている.実はこの影響がビーム揺動評価に重要だったりする.

図7: 発熱分布
・まとめ
・今後の予定
ビームが伝搬にしたがい減衰する効果を取り入れたい.In-Formでできることは分かっているのだが,少々面倒なスクリプトを組まなくてはならない.