物理実験3(SP)
指定教科書
 |
「物理実験3」 東海大学理学部物理学科 実験指導書は受講者に無料で配布されます. (表紙の色は毎年異なります) |
関数電卓の選び方,使い方
→こちらに解説があります.
概要
「物理実験3」は,主に5セメスターの皆さんを対象に開講されています. 1,2年で履修してきた「実験1」,「実験2」との違いは,一つのテーマを3週間かけてじっくり行うと言うことで,より高度で実践的なテーマについて学習します.「実験1」,「実験2」と違い選択授業ですが,その重要性を考えれば,全員が是非履修するべきものです.実験テーマは,以下のルールの下である程度は選べるようになっています.以下の,各テーマの概要を読み,アンケート用紙に記入してガイダンス終了時に提出して下さい.
実験テーマの解説
選び方のルール
下で紹介する5テーマのうち4テーマを,おのおの3週間ずつ行います.「量子基礎」は基礎テーマとして全員が履修します.残り4テーマから,特に履修を希望するテーマを1つ選んで下さい.残りは人数のバランスを考え自動的に決定されます.
量子基礎 プランク定数の測定,ホール効果
量子論は,相対論と並んで20世紀最大の発見であることは疑いない.そしてそのパラダイムは我々の常識を根底から変えることになった.例えば光は波であると同時に,エネルギーhnを持つ粒子として振る舞う.「半導体」もまた量子力学無しには説明できない概念だが,なかでも「正孔」という仮想粒子が確かに電流を担っていることをホール効果の測定により確認することができる.
(1) 光電効果の観測とプランク定数の決定
(2) p形半導体,n形半導体とホール効果の測定
(3) レポート作成
分子複雑系の物性 熱分析,電磁波分光, ボルツマン定数の測定
単純液体とよばれる理想液体や固体とは違って,ほとんどの液体や固液中間体は複雑系と呼ばれる物質群である.生命現象はこれら複雑系の高度な物性・機能から発現している.ここでは熱や電場,光を複雑系物質(水素結合性液体,液晶,プラスチック,タンパク質など)に与え,その応答を計測・解析することで,「比熱と相転移」「複素誘電率」「拡散係数と分子サイズ」などといった複雑系物質の基礎物性とその計測法を学ぶ.
(1) 相転移現象と複素誘電率の測定
(2) 拡散係数と分子サイズ測定
(3) ブラウン運動の解析によるボルツマン定数の測定
光,電磁波 レーザーと偏光に関する実験
このテーマでは,光に関する基本的な性質を理解するための実験を行います.光は電磁波であり,そのために「直線偏光」「円偏光」のような性質が現れ,また電磁波であるがゆえに「反射」「屈折」がMaxwellの方程式で説明できることを理解します.Fresnelの法則,複素屈折率,高分子溶液の「旋光性」などを,レーザーを使った教材で確認します.
(1) 直線偏光,円偏光
(2) Fresnel反射,ブリュースタ角
(3) 旋光性
放射線 放射線計測
原子核の崩壊および放射線の性質に関する基礎的なテーマを扱う.具体的には,シンチレーション検出器を用いたガンマ線スペクトロスコピーの測定を通じて,ガンマ線と物質の相互作用(光電効果,コンプトン散乱,電子陽電子対生成)や吸収・散乱などの性質を学ぶ.測定器の取扱いやデータの統計処理・誤差の扱いなど,「ガンマ線天文学」のみならず,他分野に通じる実験の基本事項も多く含んでいる.
(1) ガンマ線と物質の相互作用
(2) ガンマ線の吸収係数,強度の距離による逆2乗則
(3) MCAを用いたガンマ線スペクトロスコピー
プラズマ プラズマ生成と診断に関する実験
電離気体であるプラズマは,原子・分子等による粒子的性質だけでなく集団的性質や電磁流体的な性質も示すため,プラズマ特有の複雑な挙動を示す.このテーマでは,プラズマ物理の紹介,真空技術,プラズマ発生機構,さらには基本的な物理量である密度と温度の診断として粒子計測法と分光計測法について学ぶ.
(1) プラズマの生成と真空技術
(2) 粒子計測法によるプラズマ診断
(3) 分光計測法によるプラズマ診断
メールでの質問
偏光・反射の法則
|
|
1. 目 的 光が電磁波の一種であり,それゆえ偏光という性質が現れることを理解する.光の偏光をあやつるツールである「偏光板」「l /2板」「l /4板」の原理および使い方を理解する.
2.解 説
a 光の正体
光の正体は何かという議論は,有史以来物理学の最大の興味であり,謎であった.光が波のような性質を持つこと,即ち回折や反射,屈折という性質を持つことは古くから知られていたが,光を波と考えると,当時の物理学では説明できない最大の困難にぶつかる.即ち,光は,真空中をも伝わることが観測されているのである.
波動という現象を説明するには三つの要素が必要である.即ち
· 振動する源
· 振動する媒質
· 振幅となる物理量
である.空気中を伝わる,救急車のサイレンの音を考えてみよう.この場合振動する源はサイレン,より正確に言うなら振動する膜である.これが空気という媒質を振動させ,波動が空気中を伝搬する.振幅となる物理量は,空気の圧力の微細な変化である.これを光に置き換えると,振動する媒質と振幅となる物理量が皆目わからない.なにしろ,何も存在しないからこそ真空なのだから.
この疑問に決着をつけたのが,イギリスの大物理学者マクスウェル(J. C. Maxwell)である.マクスウェルは,1865年に,これまで知られていた電磁気学の法則の全てを,4つの基本公式にまとめた.
![]() (1.1)
(1.1)
![]() (1.4)
(1.4)
r 電荷密度 J 電流密度
E 電場ベクトル H 磁場ベクトル
D 電束密度ベクトル (=eE) B 磁束密度ベクトル (=mH)
e,mは媒体に固有の定数.
これが,マクスウェル方程式として知られている公式群である.マクスウェル方程式は暗に特殊相対性理論の正しさを要求しており,現在までこの方程式に違反する現象は見つかっていない.この公式は,電場Eと磁場Hに関する連立微分方程式であるが,この公式を変形すると波動解が現れることをマクスウェル自身が発見した.そして,その結果,波の進行速度が,当時機械的な方法で計測されていた光の速さにぴたりと一致したのである.光の速さを測る方法の歴史は,これまた非常に面白い科学史の話題であるが,ここでは割愛しよう.
電気力線,磁力線も真空中を伝わること,光が電気双極子の振動から発せられるということをあわせて考えると,光は電磁波の一種に間違いが無いと言うことになった.ここに,物理学最大の難問に決着がついたというわけである.
b 光の性質
光が電磁波であることから,光の性質を調べるためにまず一般の電磁波の性質から考えよう.マクスウェル方程式の波動解のうち,最も単純なものが平面波という解である.いま,z方向に伝搬し,電場がx方向に振動するような解を考えよう.その数式的表現は以下のようになる.
![]() (1.6)
(1.6)
w 電磁波の角振動数 k 電磁波の伝搬定数,または波数
この式をマクスウェル方程式から導出する手順については章末の付録を参照してほしい.このとき,伝搬定数kは,光の角振動数w,光の位相速度cと以下の関係にある.
![]() (1.7)
(1.7)
kの単位はMKS系では[m−1]で,1mあたりの「山」の数に2pを掛けた量になる.
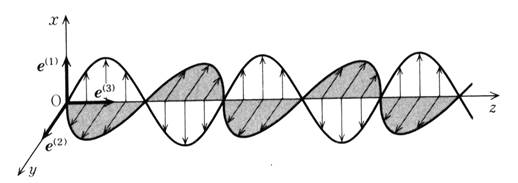
図2: よくある平面波の図式的表現
z方向に進行する平面波をあるxy平面で見ると,その面の電場強度はあらゆる場所で一様である.従って,平面波は無限に広い空間を占める.もちろん,こんな電磁波は実際には存在できないが,電磁場分布が非常に単純であるので,ここからはしばらく平面波を例にとって考えよう.非常によく見かける平面波の図式的表現は図2のようなものだが,これは,電磁波の空間的な広がりを全く無視して描かれていることに注意するべきである.
電磁波の進む速さcは,マクスウェル方程式を解けば,電磁波が伝わる媒質の誘電率e,透磁率mの関数で
と表されることが示される(章末の付録を参照).もちろん,真空の誘電率,真空の透磁率を代入すれば有名な物理定数c=299 792 458 m/sを得る.
c 偏光板
自然界に存在するあらゆる光は,理論的には平面波の重ね合わせで表わされることが知られている.ということは自然界の光をより単純な要素に分解することも可能であろう.光を振動数に分ける話は別の機会に勉強してもらうとして,この実験は光を偏波に分けることを考える.
式(1.5),式(1.6)の電磁波はz方向に進行する,存在可能な電磁波の一つだが,これだけが可能な解ではない.z方向に進むという制限を与えても,電場の振動方向はxy面のあらゆる方向に可能である.そして,我々が見ているほとんどの光は,実際に電場はあらゆる方向に,ランダムに振動している.これをランダム偏光と呼ぼう.我々がはじめに学ぶのは,ランダム偏光の光から特定の方向の振動の光のみを取り出す道具,偏光板である.
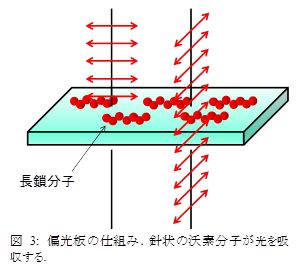 偏光板とは,図3のように,一方向に揃った長い分子を含む樹脂でできている(他にも偏光板になる物質はいろいろあるがここでは触れない).ランダム偏光を偏光板に通すと,偏光板の中に分散した吸収体分子の方向に振動する電場は吸収され,直角方向に振動する電場のみが通過する.こうして得られた光は直線偏光と言う.
偏光板とは,図3のように,一方向に揃った長い分子を含む樹脂でできている(他にも偏光板になる物質はいろいろあるがここでは触れない).ランダム偏光を偏光板に通すと,偏光板の中に分散した吸収体分子の方向に振動する電場は吸収され,直角方向に振動する電場のみが通過する.こうして得られた光は直線偏光と言う.
身近なところでは,セロハンテープがその製造工程のためにいくらか偏光板の性質を持っている.あとで,実験1をセロハンテープでやってみよう.人間の目は光の偏光を検出することができないので,偏光板を通過したランダム偏光の光はもとの光と何ら変わらないように見える.唯一の違いは,強度が弱くなっていることである.計測すれば強度が1/2になっていることがわかるが,この理由を説明できるかな?
d 光電場の分解,合成
さて,偏光板を通った結果得られた,一見何の変化もない直線偏光だが,その性質はもう一枚の偏光板を使えば明らかになる.直線偏光を偏光板に通した場合,偏光の向きと偏光板の向きの相対角度によってどのようなことが起こるかを予想しよう.電磁波の電場はベクトル量であるから,「ベクトル分解・合成」を使えば簡単に答えられる.
いま,図4の(a)の様に,x軸に対して角度qで偏光板に入射する偏光を考える.偏光板を通過したあとの電磁波はどのような偏光方向,強度を持つだろうか.この疑問に答えるために,電場を(b)のような二つのベクトルに分解する.偏光板の透過方向と垂直な方向を基準に取り,電場のなす角をqとすると,それぞれの大きさは

図4: x軸に角度qをなす電場をx方向の電場とy方向の電場に分解する
![]() (1.9)
(1.9)
![]() (1.10)
(1.10)
である.物理の法則は(a)のベクトルを(b)のような二つのベクトルの合成と見ても等しく成立するから,これらの電場が偏光板に入射すると,偏光板の透過方向に平行なベクトルのみが通過する.通過した電場の大きさは
![]() (1.11)
(1.11)
となる.
一般的に光検出器は,光電場の二乗に比例した感度を持つ(つまり,光のパワーに比例した感度を持つ)ので,検出器の出力をqの関数で表すと
![]() (1.12)
(1.12)
となる.すなわち,直線偏光を更に偏光板に通すと,電場の方向が偏光板の透過方向に一致した成分,即ち元の光と同じ強さか,それより弱い光が通過すると言うことが分かる.![]() となる角度を選べば光は全く通過しない.
となる角度を選べば光は全く通過しない.
e l/2板
 任意の直線偏光は,二つの直交する直線偏光に分解できることがわかった.次に,分解したベクトルを足しあわせるときに,すこし面白い素子を使おう.図5は,「l/2板」という素子である.ただの透明な板に見えるが,その正体は複屈折効果を持つある種の結晶である.結晶は原子が規則正しく並んでできているのは諸君も知っていると思うが,この並びの軸方向と光の電場ベクトルの相対的な角度によって,結晶中を進む光の速さが異なるという現象が観測される.これを「複屈折」という.
任意の直線偏光は,二つの直交する直線偏光に分解できることがわかった.次に,分解したベクトルを足しあわせるときに,すこし面白い素子を使おう.図5は,「l/2板」という素子である.ただの透明な板に見えるが,その正体は複屈折効果を持つある種の結晶である.結晶は原子が規則正しく並んでできているのは諸君も知っていると思うが,この並びの軸方向と光の電場ベクトルの相対的な角度によって,結晶中を進む光の速さが異なるという現象が観測される.これを「複屈折」という.
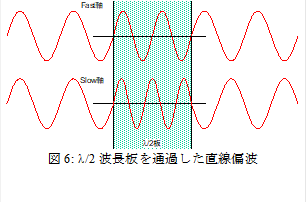
l/2板には直交する二つの軸があり,一つをslow軸,もう一つをfast軸と呼ぶ.slowとfastは,その方向に電場が向いた直線偏光が早く進むか,遅く進むかという意味で名付けられている.さて,この結晶は,ある波長で,slow軸に沿った振動方向の光とfast軸に沿った振動方向の光が同時に入射したとき,出口で図6の様にちょうどl/2の位相差が生じるように厚さが定められている.波は,速度が変化しても周波数が変化することはないので,速度が早いほうがより少ない振動数で出口に達する.
次に,この結晶に,fast軸に対して任意の角度qで入射する直線偏波に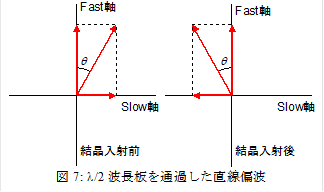
 |
ついて考えよう.先ほどと同様,図7左の様にやってきた光をslow軸方向とfast軸方向に分けて,それぞれの振る舞いについて考えればよい.結晶出口では,図7右の様にfast軸の位相は変化しないのに対して,slow軸の位相は180º反転する[1].すると,合成されてできた直線偏光は,元の直線偏光とfast軸を基準に裏返った方向に振動することになる.これは,直線偏光の振動の向きが2q回転したと言い換えても良い.
直線偏光の向きがちょうどfast軸に一致するときはslow軸成分は無いわけだから,結晶を通過した後の偏光面(電場振動方向)の回転はない.
このように考えると,l/2板は「入射した直線偏波の偏光方向を任意に回転させる素子」と言える.これがどのように使えるか考えてみよう.いま,諸君の目の前にあるHe-Neレーザーは,鉛直方向に電場が振動する直線偏光を発している.しかし,実験の内容によっては,斜め45ºや水平方向など,任意の方向に偏波した直線偏光がほしい.このようなときはどうするか.レーザーを回転させる? もちろん正解だが,ここはスマートにl/2板を使おう.
f l/4板
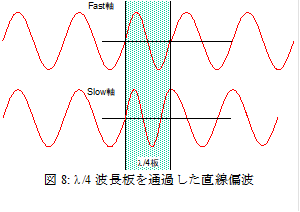 l/2板が直線偏光の向きを回転させる機能があることがわかった.次はもう少し面白い素子を使おう.l/2板と同様に重要な素子が「l/4板」である.その名前から想像できるように,l/4板はfast軸とslow軸の位相差が波長の1/4になるような板である.カンのいい諸君は気がついたかもしれないが,l/4板は単にl/2板を半分の厚みにするだけで実現できる.
l/2板が直線偏光の向きを回転させる機能があることがわかった.次はもう少し面白い素子を使おう.l/2板と同様に重要な素子が「l/4板」である.その名前から想像できるように,l/4板はfast軸とslow軸の位相差が波長の1/4になるような板である.カンのいい諸君は気がついたかもしれないが,l/4板は単にl/2板を半分の厚みにするだけで実現できる.
いま,この結晶に,slow軸とfast軸のちょうど中間の方向に振動する直線偏光を入射してみよう.この後光がどうなるかは,やはりベクトルを分解して考えればよい.入射光をslow軸に沿って進む成分とfast軸に沿って進む成分に分解する.それぞれは結晶に同時に入射し,出口では図8の様にp/2だけ位相がずれて出会うことになる.
すると,結晶を出た光の電場ベクトルは,もはや直線偏光とはならない.光の進行方向に垂直なxy平面で,電場ベクトルの時間変化を追ってみよう.すると図9のように,電場ベクトルは円を描くように変化することがわかる.このような光を「円偏光」という.入射する直線偏光がちょうどslow軸とfast軸の中間でなく,その間にあるときは,射出光は「楕円偏光」になる.
一端を壁に取り付けられたロープのもう一端を持ち,ピンと張ろう.ロープを持った手を振ると,ロープに進行波が現れる.手を上下に振った状態の振動が直線偏光で,手をぐるぐる回転させたときの振動が円偏光になる.
さて,ここで,今見ている光が円偏光,楕円偏光であることをどうやって確かめたら良いだろうか.我々には電場ベクトルが回転しているのを見る能力はないが,偏光板を使うことはできる.偏光板は,任意の電場ベクトルから,偏光板の方向に振動する直線偏光成分だけを取り出すことができることを思い出そう.
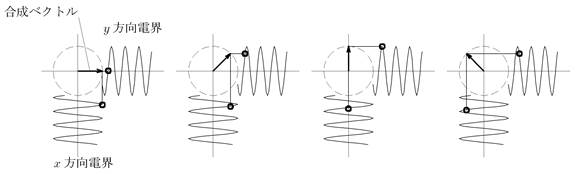
図9: x方向電場の振動とy方向電場の振動を,![]() だけ位相をずらし重ね合わせた様子
だけ位相をずらし重ね合わせた様子
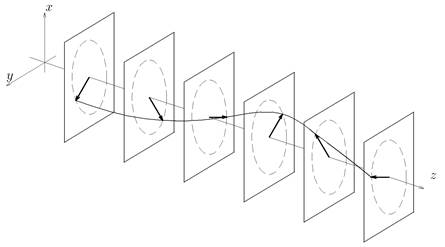
図10: z軸に沿って進む円偏波の電場ベクトルを,ある瞬間で固定したもの
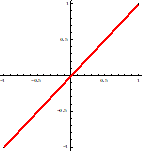
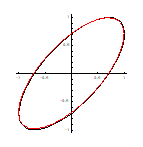
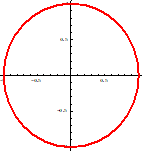
直線偏光: 位相差0 楕円偏光: 位相差p/4 円偏光: 位相差p/2
図11: 直線偏光,楕円偏光,円偏光
実 験 装 置
・ He-Neレーザー:単色,直線偏光の光を出すツール.
・ 偏光板:ある特定の方向の直線偏光のみを透過させる板.
・ ターンテーブル:試料を置き,精密に角度を計測しつつ回転できる.アームがあり,先端には偏光板(回転目盛つき)と光検出器が装着されている.
・ 光検出器:シリコンフォトダイオードにより光パワーを検出する.
・ l/2板:直線偏光の偏光面を任意に回転させる板.Fast軸とSlow軸の位相差が入口と出口でl/2になるよう設計されているためこの名前がある.
・ l/4板:直線偏光から円偏光を作る板.Fast軸とSlow軸の位相差が入口と出口でl/4になるよう設計されているためこの名前がある.
手 順
実験1: 偏光板を使った実験
(a) 肉眼による観察
偏光板を2枚手に持ち,部屋の蛍光灯を見る.まず偏光板1枚を通して,蛍光灯を見てみよう.蛍光灯の明るさはどのように変化したか?また,偏光板を回転させてみよう.蛍光灯の明るさは変化したか?
続いて,偏光板を2枚重ねてみよう.2枚目の偏光板を回転させ,互いの角度を変えてみよう.蛍光灯の明かりは,どのように変化するか観察してみよう.
(b) 偏光サングラスの実験
サングラスの仲間で,特に「偏光サングラス」と呼ばれるものがある.これは主に自動車の運転,釣りやマリンスポーツの際に威力を発揮するサングラスである.第2週で詳しく説明するが,斜め45ºくらいの角度で太陽光がガラスや水面に当たり,反射してこちらに向かってくるときその偏光はほぼ直線偏光と考えて良い.一方,透過光は全ての偏光をまんべんなく含む.したがって,反射光の偏光と垂直な偏光のみを通す偏光板を通すと,まぶしい太陽光はほぼ遮断され,ガラスや水面の境界を通り抜けた光は半分だけ透過する.つまり,太陽光の反射に邪魔されずに向こう側が見えるというわけだ.これを実際に確認してみよう.
(c) 直線偏波光と偏光板の角度
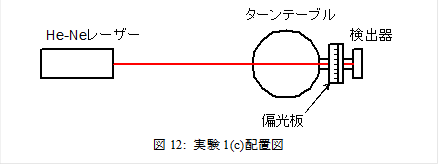 |
図12は実験装置の配置図である.He-Neレーザーは,地面に垂直に振動する直線偏波の光を発生している.偏光板を回転させつつ,角度15ºおきに光強度を計測してみよう.偏光板の角度と,検出光の強度の関係をグラフにしなさい.
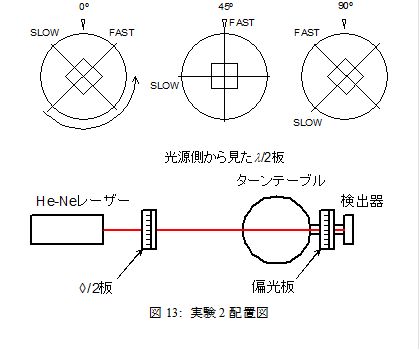 |
実験2: l/2板を使った実験
図13のように,He-Neレーザーの直後にl/2板を置く.はじめに角度目盛を0にセットする.このとき,l/2板のslow軸とfast軸はレーザーの偏光に対してそれぞれ±45ºになっている.l/2板を通ったレーザーの偏波はどのように変化しているか,手持ちの偏光板で確認せよ.続いて,検出器手前の偏光板を回転させる.あるところで検出器の出力がほとんど0になるはずである(完全に0にならないのは素子の不完全さによる).これは何を意味するかというと,偏光板の向きと直線偏光の向きが直交し,全てのレーザー光が遮られたということである.すなわち,偏光板を使えば,直線偏波がどちらの方向に振動しているかを正確に知ることができるわけだ.今回のように,偏光板を偏光方向に一致させるのでなく直交させるのは,偏光の向きを精密に知るためである(理由を考えよ).
続いて,角度目盛りを10ºにセットしよう.すると,検出器の出力が変化する.しかし,偏光板をわずかに回転させると,再び検出光の強度がほぼ0になる.このときの偏光板の目盛りは,始めの状態からどれほど変わったか.
方眼紙を用意し,横軸にl/2板の角度目盛り,縦軸に偏光板の角度目盛りを取ってグラフを描きなさい.l /2板の角度は0から90ºまで変化させること.
実験3: l/4板を使った実験
図14のように,実験2のセットアップに加えて光路にl/4板を挿入する.実験2の結果から,l/2板の角度を変えることで任意の方向に偏波した直線偏光が得られることが分かっている.l/2板は,目盛りを0ºに合わせると射出光が水平な偏波に,45ºに合わせると鉛直な偏波になる様に調整されている.
はじめ,偏光の向きを鉛直にセットする.この位置を,この実験における「条件1」とする.l/4板は,slow軸とfast軸があらかじめ地面と45ºをなすように調整されているので,自動的に入射光はslow軸成分とfast軸成分に等分される.続いて,偏光板を回転させ,15º毎に光強度を計測する.計測された光強度が,電場ベクトルの,その方向の成分の二乗である.配られた円グラフに,角度と光強度の関係を記してみる.
同じ計測を,l/4板に入射する電場の方向を変えてやってみよう.電場の方向を変えるにはl /2板を回せば良いことはもう分かるね.目盛りを22.5ºにセットすると偏波面は二倍の45º回転するから,直線偏光がfast軸に一致する方向になる.この2つの条件において,円グラフを描いてみると,結果は図17の様になるはずである.なぜこうなるかを定性的に説明しなさい.
時間があったら,(1)と(2)の中間の角度(3)の偏光をl/4板に入射して,楕円偏光を作ってみなさい.
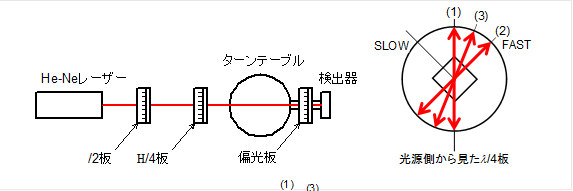 |
図14: 実験2配置図
![]() 測 定 例
測 定 例

図15: 偏光板角度と透過光パワーの関係
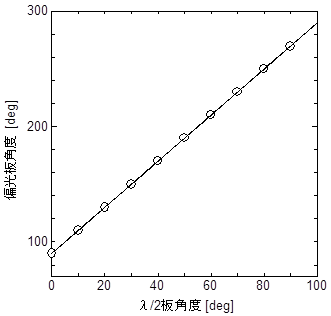
図16: l/2角度と,消光状態になる偏光板角度の関係
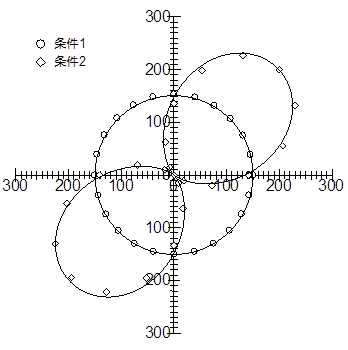
図17: l/4板に対する入射角度を変えたときの,偏光板回転角qと受光強度Iの関係
2 フレネルの反射公式
![]() 1. 目 的 光が物体に当たるとその一部が反射,残りは屈折しつつ透過する.反射・透過を支配する法則を4本の公式にまとめたフレネル(Fresnel)の公式を導出,実験により確認する.
1. 目 的 光が物体に当たるとその一部が反射,残りは屈折しつつ透過する.反射・透過を支配する法則を4本の公式にまとめたフレネル(Fresnel)の公式を導出,実験により確認する.
2.解 説
a 光の反射
光を透過する物性を特徴づける性質として,屈折率が定義されている.これは,斜めに入射する光線が,境界面でどの程度曲がるかを示す定数で,スネル(Snell)の法則といわれる以下の公式で関係づけられている.
ここでn1,n2が光が伝わる媒質の屈折率で,界面に対して角度q1で入射した光は,式(2.1)で表される角度q2で屈折率n2の媒質を伝搬する.
一方,電磁波が伝搬する媒質の性質は媒質の誘電率,透磁率で表すことができる.ところが,簡単な考察により,この屈折率が,物質の誘電率と
の関係で関係づけられることが示される.ここで,![]() は物質の誘電率を真空の誘電率
は物質の誘電率を真空の誘電率![]() で規格化したもので,比誘電率と言う.その理由を説明しよう.
で規格化したもので,比誘電率と言う.その理由を説明しよう.
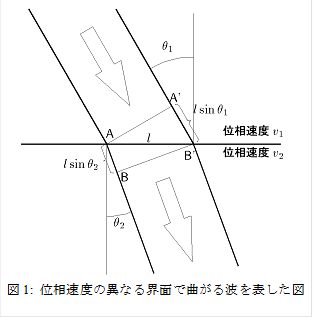
一般に(電磁波に限らず)波がその位相速度の異なる境界に斜めに入射すると,その進行方向が曲がることが示される.これは,速度の異なる界面でも波が連続であるということから説明できる.図1から,角度q1,q2と波の位相速度の間には
の関係があることがすぐにわかるだろう.証明は簡単なので挑戦して見よう.続いて,物質中の光の速度を真空の速度に対する相対値で表してみよう.電磁波の進行速度が式(1.8)で表されることは既に述べたが,光の周波数になると,ほとんどの物質の透磁率は真空の透磁率m0に等しくなる.これは,分子,原子の磁気双極子の反転が光の周波数(1015Hz程度)に追いつかないためである.従って,物質中の光速度は
と表すことができる.これを式(2.3)に代入すると
![]() (2.5)
(2.5)
が得られ,![]() が屈折率と言う言葉で古くからなれ親しまれていたものと同じ値になることがわかる.
が屈折率と言う言葉で古くからなれ親しまれていたものと同じ値になることがわかる.
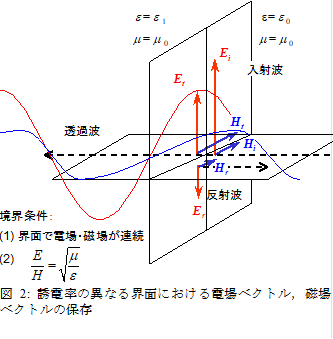 続いて,真空と物質の界面で保存される量について考察しよう.電磁気学の教えるところによると,物性の異なる界面に沿う電場ベクトルEは,界面の両側で保存される.また,界面に沿う磁場ベクトルHも,界面の両側で保存される.ところが,先に述べたように,マクスウェル方程式によると,電磁波の電場ベクトルと磁場ベクトルの比率は一定の値をとり,それは物質の誘電率,透磁率の関数で以下のように表される(章末の証明を参照).
続いて,真空と物質の界面で保存される量について考察しよう.電磁気学の教えるところによると,物性の異なる界面に沿う電場ベクトルEは,界面の両側で保存される.また,界面に沿う磁場ベクトルHも,界面の両側で保存される.ところが,先に述べたように,マクスウェル方程式によると,電磁波の電場ベクトルと磁場ベクトルの比率は一定の値をとり,それは物質の誘電率,透磁率の関数で以下のように表される(章末の証明を参照).
![]() (2.6)
(2.6)
![]() は電磁波媒体の特性インピーダンスhと呼ばれる.すると,誘電率の異なる界面に電磁波が入射するとき,その両側で(E/H)の比率が異なるわけだから,電場と磁場の保存則を同時に満たすのは不可能となる.その結果,何が起こるかというと,電磁波の反射が起こるというわけである.
は電磁波媒体の特性インピーダンスhと呼ばれる.すると,誘電率の異なる界面に電磁波が入射するとき,その両側で(E/H)の比率が異なるわけだから,電場と磁場の保存則を同時に満たすのは不可能となる.その結果,何が起こるかというと,電磁波の反射が起こるというわけである.
いま,電磁波が真空から物体に向かって入射するとしよう.このとき,真空の側に,入射波と反対側に進行する平面波が入射波と同時に存在すれば,これらを合成した電場と磁場が常に物質側の値と一致しつつ,全ての電場/磁場の比率が![]() を満足することが可能である.これが,光が,誘電率(屈折率)の異なる界面で反射する理由である.これをフレネル反射という.フレネル反射は,ガラスに自分の姿が映るという現象で,日常的に観測できる.
を満足することが可能である.これが,光が,誘電率(屈折率)の異なる界面で反射する理由である.これをフレネル反射という.フレネル反射は,ガラスに自分の姿が映るという現象で,日常的に観測できる.
b フレネルの反射公式
一方,界面に対して斜めに入射した電磁波がどの程度反射されるかということは,光の入射角qと,電場,磁場が保存則を満足するという条件から導くことができる.ここで,話を直線偏光に限定しよう.どんな光波も直線偏光にベクトル分解できるので,これによって一般性が損なわれるわけではない.更に,物質の界面に対して,「電場ベクトルが平行」の場合と「磁場ベクトルが平行」の場合と,2種類のみを考えれば充分であることは,ベクトル合成の考え方から明らかであろう.一般的に使われている呼び名は,電場が界面に平行な電磁波がTransverse Electric WaveまたはTE波,磁場が界面に平行なものがTransverse Magnetic WaveまたはTM波である.
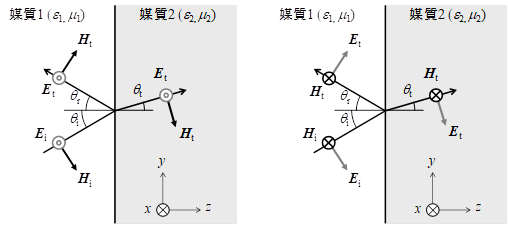
図3(a): TE波(s偏光)の電場,磁場の向き 図3(b): TM波(p偏光)の電場,磁場の向き
ところで,上の定義は,主に電波の技術者たちが好んで使ってきた定義で,光学の分野では伝統的にp偏光,s偏光という言い方が使われてきた.pとは,ドイツ語の“parallel”(平行な)の略で,TM波のことを指す.一体,何が何に平行かというと,p偏光は,入射波と反射波を含む面,つまり図3(b)の様に,紙面に電場ベクトルが平行という意味である.一方のs偏光はドイツ語のsenkrecht(垂直な)の略で,これは当然TE波を指す.s偏光は,電場ベクトルが図3(a)の様に紙面に垂直な偏光である.これらの定義がスタンダードになった背景には,当時ドイツが光学の分野で世界をリードしていたという事実がある.光周波数の電磁波を議論するときには,現在でもほとんどp偏光,s偏光が使われる.ある物理的性質を表すのに複数の定義が存在するのは,科学が常に進歩するということから止むを得ないことであるが,是非混乱しないで使いこなして欲しい.
s偏光(TE波)がある角度qiで界面に当たるとき,入射,反射,透過電場が満たすべき条件は図3(a)から以下のようになる.
電場の境界条件:![]() (2.7)
(2.7)
式(2.8)は,磁場のy方向成分を考え,さらに電場と磁場の比率が以下の関係で表されることに気が付けば導出できる.ただしここで反射の法則すなわちqi= qrを天下りに導入している[2].
真空側:![]() → H(真空)=E(真空)×
→ H(真空)=E(真空)×![]()
物質側:![]() → H(物質)=E(物質)×
→ H(物質)=E(物質)×![]()
境界条件:Hy (入射波)+ Hy (反射波)= Hy(透過波)
![]() (符号に注意)
(符号に注意)
両辺を![]() で割れば式(2.8)を得る.ここからEtを消去し,反射率Er/Eiを求めてみよう.
で割れば式(2.8)を得る.ここからEtを消去し,反射率Er/Eiを求めてみよう.
![]()
更に,スネルの法則を使ってnを消去すると
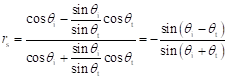 (2.10)
(2.10)
を得る.p偏光(TM波)の場合も同様に,入射,反射,透過電場の満たすべき条件は
電場の境界条件:![]() (2.11)
(2.11)
磁場の境界条件:![]() (2.12)
(2.12)
ここからEtを消去し,反射率Er/Eiを求めてみよう.
![]()
更に,スネルの法則を使ってnを消去すると
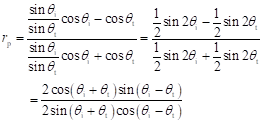
を得る.透過率も同様に計算することができて,これらをまとめたものが以下のフレネルの反射公式として知られている.
フレネルの反射公式
![]() (2.17)
(2.17)
![]() (2.18)
(2.18)
c ブリュースタ角
p偏光(TM波)の反射率を角度の関数として計算すると,ある点で,反射率が0になることに気づいただろうか.この特別な角度はブリュースタ角(Brewster’s
angle)と呼ばれる.ブリュースタ角で取り付けられた窓は,p偏光に対して一切の反射がない.これは,光学の分野で非常に応用が広い物理現象である.ある入射角でp偏光の反射率が0になることは,式(2.14)から明らかで,![]() なる角度において分母が無限大になる.逆に,屈折率からブリュース
なる角度において分母が無限大になる.逆に,屈折率からブリュース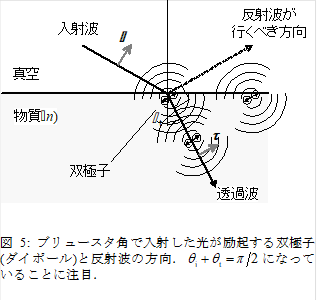
 タ角を導くことも可能で,結果だけ示すと
タ角を導くことも可能で,結果だけ示すと
qB 真空から屈折率nの誘電体に光が入射するときのブリュースタ角
n 誘電体の屈折率
となる.
ブリュースタ角で反射率が0になることを,簡単な物理的考察から導こう.物質内部を伝搬する波は,光の電場によって物質を構成する分子の双極子が振動し,その振動が新たな光電場を作り出して次々とリレーすることにより伝搬しているのだ,という解釈がある.一方,振動する双極子の放射する電場は,図4の様な強度分布を持っている.図4から,双極子の放射する電磁波には強度分布に偏りがあることがわかるだろう.ちょうど,北極と南極方向には電磁波のエネルギーは放射されない.これは,光が横波であるということから簡単に説明できる.波は,ゆする方向と直角に進むのである.一方,図5のようにブリュースタ角で物質に入射した電磁波を考えよう.この電磁波は,物質表面の原子を振動させ,この原子は双極子放射によって透過波,反射波を作る.ところが,反射波が行くべき方向は,ちょうどこの双極子にとって北極方向,即ち電磁波が放出されない方向に一致する.このように,ブリュースタ角で入射したp偏光は,反射波を作ることができないと言うことが説明できた.
![]()
実 験 装 置
・ He-Neレーザー:単色,直線偏光の光を出すツール.
・ 偏光板:ある特定の方向の直線偏光のみを透過させる板.
・ ターンテーブル:試料を置き,精密に角度を計測しつつ回転できる.アームがあり,先端には光検出器が装着されている.
・ 光検出器:シリコンフォトダイオードにより光パワーを検出する.
・ l/2板:直線偏光の偏光面を任意に回転させる板.Fast軸とSlow軸の位相差が入口と出口でl/2になるよう設計されているためこの名前がある.
・ 試料台:試料であるガラス板を固定する.ターンテーブルのピンにはまる穴が開いている.
・ ガラス板:フレネルの法則を計測する対象.不要な反射を防ぐため裏面はスリガラスになっている.
![]() 手 順
手 順
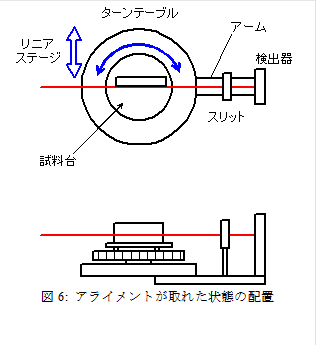
1: アライメントとテーブルの原点補正
A) アライメント
アライメントとは,He-Neレーザー出た光が回転台の中央を通り,検出器の中心に当たるように機器の位置を微調整する作業である.
予めl/2板を挿入しておき,鉛直な偏光を作る(目盛り45º).この実験装置のセッティングではこれが試料に対してのs偏光となる.
 |
図6のように,レーザーから出た光が細いビームとなり,試料台にセットしたガラス板をかすめるように通り抜ける状態にする.ここで調整するのは図6の試料台の角度と図7の(A)リニアステージ(位置).薬包紙を使い,ビームの通っている場所を確認しながら調整すること.
B) ターンテーブルの原点補正
ターンテーブルには目盛りがついており,検出器の角度を計測するようになっているが,この段階ではまだ検出器は原点が正確には合っていない.次に,(B)回転ステージを使って原点の補正を行う.
(1) 試料台をターンテーブルからはずす.忘れないように!!
(2) 検出器を180.0ºの位置にセットする.He-Neビームは検出器に入射しているが,正確に中心ではない.
(3) (B)回転ステージ(図7)を回して,検出器の強度が最大になるように調整.
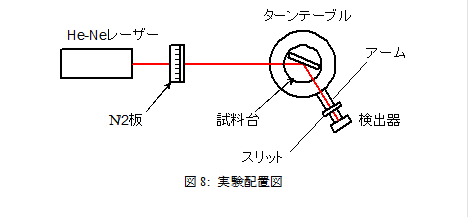
2: 測定
1. 試料台にガラス板を固定する.
2. l /2板の目盛りを45ºにセットし,ガラス板に対してs偏光の直線偏光を作る.つまり,鉛直な偏波である.
3. アライメント(前項)を行い,ターンテーブルの位置を調整する.
4. いったん試料をどけて,検出器を180°の位置にセットする.ターンテーブルの原点補正が終わったら,検出器の出力を計測する.このときのパワーが,入射する光の強度になる.
5. 入射角5°から85°の範囲で,5°刻みで反射光の強度を計測する.(目盛板は10°から170°)
(ア) 検出器位置を正確に合わせる.
(イ) アームを回転させ,光強度最強の位置を探す.
(ウ) この位置における強度を計測.
(エ) 反射光強度/入射光強度=強度反射率.
6. 強度反射率の平方根をとり,電場反射率を計算する.
7. 偏光板の角度をp偏光(0º)にセットする.
8. l//2板を0ºの位置まで回転させ,このガラス板に対してp偏光の直線偏光を作る.今度は水平な偏波.
9. 入射角5°から85°の範囲で反射光の強度を計測する.
 |
![]() 測 定 例
測 定 例
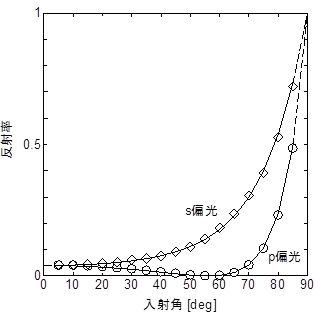
図9: 入射角と強度反射率の関係
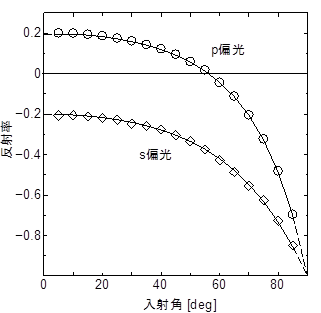
図10: 入射角と電場反射率の関係
3 複素屈折率
1. 目 的 損失のある媒体を進む光は伝播するにつれ強度が減衰する.これを,「媒質の屈折率が虚数成分を持つ」と解釈することで統一的な取り扱いを可能とするのが複素屈折率の概念である.複素屈折率を使えば,導体である金属にも屈折率が定義できること,測定手段としてエリプソメトリーという手法が知られていることを学ぶ.
2.解 説
a 波動の複素関数表示
平面波
を以下の様に表現する.
これを調和関数の複素表示(フェーザー表示)と言う.オイラーの公式,![]() があるから,この置き換えは一見正しいように見えるが,実際には式(3.1)は虚部を持たないため,この置き換えは成立しない.但しここで,「複素表示された波動の実際の姿を知るには,その実部を取れば良い」と約束する.すると,線形な演算の範囲では,複素表示された波動にどんな計算を行っても,いつでも式(3.1)の形に戻すことができる.しかし,このような置き換えにどんな意味があるのだろうか.それをこれから考えよう.
があるから,この置き換えは一見正しいように見えるが,実際には式(3.1)は虚部を持たないため,この置き換えは成立しない.但しここで,「複素表示された波動の実際の姿を知るには,その実部を取れば良い」と約束する.すると,線形な演算の範囲では,複素表示された波動にどんな計算を行っても,いつでも式(3.1)の形に戻すことができる.しかし,このような置き換えにどんな意味があるのだろうか.それをこれから考えよう.
b 損失のある媒体を進む波
一般に,波が損失のある媒質を伝搬するとき,その強度は以下のように減衰することが知られている.
![]() (3.3)
(3.3)
ここでaは減衰定数と言われる定数で,その逆数が,波の強度が1/eに減衰する距離を与える.この式を,z軸に添って進む平面波にあてはめると以下の様になる.
ここで,強度減衰率は電場減衰率の自乗なので,減衰項は1/2乗した.次に,式(3.4)を複素関数表示で表してみよう.すると,
![]()
![]()
となり,見かけ上は減衰項が複素数の伝搬定数に含まれた形を得る.つまり,損失のある媒質を進む波の振る舞いは,伝搬定数が複素数であると考えれば,損失のない媒質の場合と同じ取り扱いが可能であることがわかる.式(3.5)における伝搬定数![]() を複素伝搬定数と呼ぶ.
を複素伝搬定数と呼ぶ.
式(A8)の関係より,複素伝搬定数を与える複素誘電率![]() が必ず存在し,これを
が必ず存在し,これを
![]() (3.6)
(3.6)
と定義する(「複素透磁率」もありうるがここでは考えない).すると式(2.2)の関係から当然複素屈折率も定義される.
![]() (3.7)
(3.7)
c 複素屈折率とFresnel反射公式
いま,金属のような損失のある媒体に電磁波を入射させることを考える.このとき,s偏光,p偏光の反射率は,屈折率が複素数でもフレネルの公式に従う.式(2.9),式(2.13)はそれぞれ複素屈折率![]() を使い,
を使い,
と与えられる.式(3.8)や式(3.9)は複素数を含むため,たとえ![]() が与えられても具体的に
が与えられても具体的に![]() ,
,![]() を計算することは並大抵のことではない.しかし,最新型の関数電卓やMathematicaの様なソフトウェアを使えば,
を計算することは並大抵のことではない.しかし,最新型の関数電卓やMathematicaの様なソフトウェアを使えば,![]() ,
,![]() はどちらも絶対値が1未満の複素数として得ることができる.これを複素反射率と呼ぼう.
はどちらも絶対値が1未満の複素数として得ることができる.これを複素反射率と呼ぼう.
複素反射率とはどんな意味を持つ量だろうか.実数の反射率は,(反射波の電場)/(入射波の電場)と直感的な理解が可能である.この量が複素数になるということは,物理的には「反射波の位相が入射波に対して任意の角度だけ異なりうる」ことを意味するのである.
簡単な実験でこれを確認することができる.ある入射角で,金属に直線偏光を入射させる.このとき,直線偏光は入射面に対してs偏光とp偏光を同じ量だけ含む直線偏光とする.すると,![]() ,
,![]() が大きさだけでなく位相も異なるため,反射した光はs偏光とp偏光が異なる位相で振動することになる.異なる位相で振動する二つの直線偏光を重ね合わせると楕円偏光になることは1日目の実験で既に学んだので理解できると思う.今日の実験は,金属の反射率が複素数になることを確認し,そこから金属の複素屈折率を決定することを目的とする.
が大きさだけでなく位相も異なるため,反射した光はs偏光とp偏光が異なる位相で振動することになる.異なる位相で振動する二つの直線偏光を重ね合わせると楕円偏光になることは1日目の実験で既に学んだので理解できると思う.今日の実験は,金属の反射率が複素数になることを確認し,そこから金属の複素屈折率を決定することを目的とする.
c エリプソメトリー
ここでは得られた反射率のデータから金属の複素屈折率を計算する方法について述べる.ここから先は相当面倒な計算になるので,わからなくても悲観することはない.言われたとおりに計算すれば得られるのは金属の![]() であり,金属にもガラスやプラスチックなどと同様に物質固有の屈折率が定義されるということを理解できれば良い.
であり,金属にもガラスやプラスチックなどと同様に物質固有の屈折率が定義されるということを理解できれば良い.
始めに行うことは,金属に当たって反射した光がどのような楕円偏光になっているかを調べることだ.そのため,金属に対して1日目の実験3と同じ計測を行う.偏光板の回転によって得られたデータは,偏光板の角度ごとの検出光強度で,図1(左)の様な形になるはずだ.
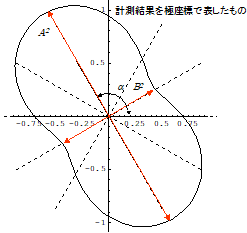
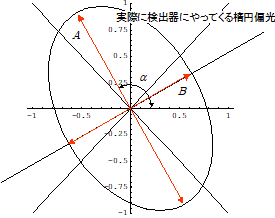
図1: 楕円偏光に対して行った計測の結果(左)と,そこから逆算した楕円偏光(右)
1日目の実験結果から明らかなように,この計測結果はそのまま偏光を表しているわけではない.実際にやってきたのは楕円偏光だから,計測結果から楕円偏光の傾斜角aと楕円率A/Bを求めよう.
Ø ひょうたん型の長軸,短軸の方向,すなわち,プロットの原点からの距離が最大,最小の方向を定める.これらは必ず直交する.
Ø 長軸の方向が楕円の傾斜角aを,長軸/長軸が(A/B)2を表す.
この方法で角aと(A/B)2が求められるのは,楕円偏光が互いに直交し,図1の楕円の長軸,短軸方向を向いた大きさA,Bの二つの電場が![]() の位相差で重ね合わされたものと見なせるためである.ただし,今日の実験では,直感的だが不正確な円グラフではなく,正確な直交グラフを使う.例を図2に示す.
の位相差で重ね合わされたものと見なせるためである.ただし,今日の実験では,直感的だが不正確な円グラフではなく,正確な直交グラフを使う.例を図2に示す.
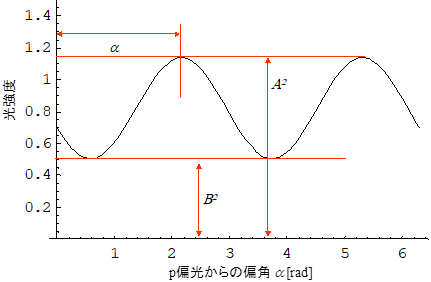
図2: 直感的ではないが,より正確なA2,B2,aの求め方
このようにして,我々は金属板からの反射光の測定から,楕円偏光の傾斜角aと楕円率(A/B)の自乗を得た.これが本日の実験から得られた直接の観測結果である.
さて,反射光は,もともとはそれぞれx方向,y方向を向いた強度,位相の等しい二つの直線偏光であったことを思い出そう.すなわち射出光の楕円偏光は,
![]() (3.10)
(3.10)
![]() (3.11)
(3.11)
という電場の合成の結果として得られたものである.rs,rpが複素数であるためにExの振動とEyの振動に位相差が現れ,合成電場ベクトルは楕円の軌道を描く.いま,複素反射率をそれぞれ
![]() (3.12)
(3.12)
![]() (3.13)
(3.13)
と,極形式で表現する.すると,楕円偏光の電場は
![]() (3.14)
(3.14)
![]() (3.15)
(3.15)
と表される.
次に,測定により得られたaと(A/B)2から,p偏光反射率とs偏光反射率に関係する物理量を得る方法を考えよう.まず,p偏光反射率とs偏光反射率の比率をとる.ここで,分かり易いように![]() ,
,![]() を定義しておく.
を定義しておく.
次に,図3の関係から,楕円偏光を,EA方向の電場ベクトルとEB方向の電場ベクトルが位相差![]() で合成されたものと考え,さらにベクトルEAとベクトルEBはそれぞれx軸方向とy軸方向電場に分解できるため,以下の関係が成立する.
で合成されたものと考え,さらにベクトルEAとベクトルEBはそれぞれx軸方向とy軸方向電場に分解できるため,以下の関係が成立する.
![]()
![]()
![]() (3.17)
(3.17)
![]()
![]()
![]() (3.18)
(3.18)
![]()
![]() (3.20) [3]
(3.20) [3]
![]()
![]() (3.21)
(3.21)
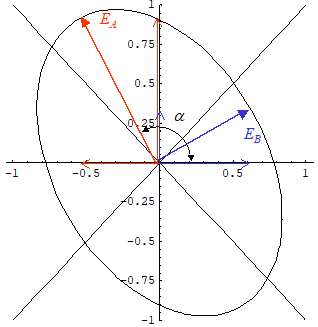
図3: EA,EBとExとEyの関係
このようにして,測定結果から我々が得たデータはP,Dという二つの量である.驚くべきことに,ここから金属の複素屈折率![]() を計算で求めることができる.手順を追ってみよう.式(3.16)とフレネルの公式(2.15) ,(2.16)の関係より,
を計算で求めることができる.手順を追ってみよう.式(3.16)とフレネルの公式(2.15) ,(2.16)の関係より,
であることがわかる.式(3.22)のqtをスネルの法則![]() を使ってqiで表せば,計測可能な量と複素屈折率
を使ってqiで表せば,計測可能な量と複素屈折率![]() のみの式になるので,原理的にはこれを
のみの式になるので,原理的にはこれを![]() について解けば
について解けば![]() が知れる.しかしqtが残念ながら複素数なので計算は非常に繁雑になる.そこで,次のような工夫をする.
が知れる.しかしqtが残念ながら複素数なので計算は非常に繁雑になる.そこで,次のような工夫をする.
まず,式![]() を定義し,式(3.22)の関係を使う.
を定義し,式(3.22)の関係を使う.
次に,スネルの法則![]() を変形し,sinqt,cosqtをsinqiで表す.
を変形し,sinqt,cosqtをsinqiで表す.
式(3.24),(3.25)を式(3.23)に代入すると以下の表式を得る.
![]() (3.26)
(3.26)
ここで,Pをある角度![]() のタンジェント,すなわち
のタンジェント,すなわち![]() とみなし,更に左辺にオイラーの公式を適用し,全ての項を電卓で計算可能な実数項の三角関数で表現しよう.
とみなし,更に左辺にオイラーの公式を適用し,全ての項を電卓で計算可能な実数項の三角関数で表現しよう.
![]()
![]() (3.27)
(3.27)
最終的に我々が得た結論は,
という表式である.この式に計測された値を代入し,![]() について解けば試料の複素屈折率が求められる.以上のように,楕円偏光を利用して材料の物性を計測する方法はエリプソメトリーとして知られている.
について解けば試料の複素屈折率が求められる.以上のように,楕円偏光を利用して材料の物性を計測する方法はエリプソメトリーとして知られている.
しかしの式の計算は,複素数の平方根を含むので少々厄介である.ところが,導体の可視域における複素屈折率は一般に![]() が成り立つので,式(3.28)を近似的に解く方法がある.式(3.28)を近似して
が成り立つので,式(3.28)を近似的に解く方法がある.式(3.28)を近似して
![]() (3.29)
(3.29)
と書き表せば,複素屈折率の実部,虚部はそれぞれ
と一発で計算可能である.ただし,式(3.30),式(3.31)はあくまで近似計算であり,厳密な計算もその気になれば不可能ではないという点を指摘しておこう.
図4は,様々な公刊論文より拾い集めた,純アルミのnとkを波長の関数で表したものである.金属の複素屈折率は,同じ元素を対象とした計測でも,計測条件や試料表面の状態,金属の結晶構造(たとえば鋳造,鍛造)などが異なるため,測定値に幅があることがわかる.アルミの複素屈折率に「正しい値」はなく,測定された値はある特定の試料の物性値であると言うことを理解してもらいたい.文献値におよそ合っていればよしとしよう.

図4: アルミの複素屈折率の波長依存性
L. G. Schulz et al., J. Opt. Soc. Am. A 44 p. 362 (1954).
G. Hass et al., J. Opt. Soc. Am. A 51 p. 719 (1961).
H. Ehrenreich et al., Phys. Rev. 132 p. 1918 (1963).
H. –J Hagemann et al., DESY SR-74/7 (1974).
A. C. Nyce, J. Opt. Soc. Am. A 65 p. 792 (1975).
実 験 装 置
・ He-Neレーザー:単色,直線偏光の光を出すツール.
・ 偏光板:ある特定の方向の直線偏光のみを透過させる板.
・ ターンテーブル:試料を置き,精密に角度を計測しつつ回転できる.アームがあり,スリットと偏光板(回転目盛つき)が装着できる.先端には光検出器が装着されている.
・ 光検出器:シリコンフォトダイオードにより光パワーを検出する.
・ l/2板:直線偏光の偏光面を任意に回転させる板.Fast軸とSlow軸の位相差が入口と出口でl/2になるよう設計されているためこの名前がある.
・ 試料台:試料であるアルミ板を固定する.ターンテーブルのピンにはまる穴が開いている.
・ アルミ板:複素屈折率を計測する対象.
手 順
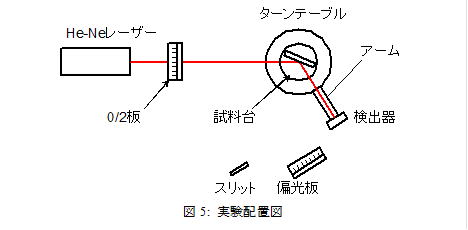 |
1: 反射の測定エリプソメトリー
1. 試料台に予め配られた試料を固定する.
2. アームにスリットを装着する.
3. l/2板の目盛りを22.5°にセットし,直線偏光の向きを,p偏光(x)とs偏光(y)が等量含まれる45ºの向きとする.
4. アライメント(2日めの手順を参照)を行い,ターンテーブルの位置を調整する.
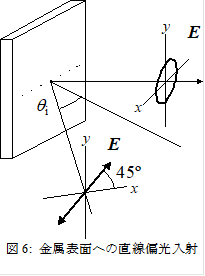 アームを回転させ,試料への入射角qiを指示された角度にセットする.
アームを回転させ,試料への入射角qiを指示された角度にセットする.
5. 試料台を回転させ,検出器に入射するパワーを最大にする.
6. アームのスリットを,回転偏光板に交換する.
7. 偏光板を回転させ,検出器で光強度を測定する.角度15º度毎の測定を行うこと.
8. 次に,アームを回転させ,試料への入射角qiを10ºにセットする.
9. 試料台を回転させ,検出器に入射するパワーを最大にする.このとき,回転偏光板は外さず,目視で試料台を回転させ,反射光を検出器に合わせること.
10. 7.と同じ測定をくり返す.
11. 横軸に偏光板回転角,縦軸に検出光強度をとったグラフを描く.
12. 図2を見ながら,(A/B)2,aを決定する.曲線の最高点および最低点は1回転に2回ずつ,それぞれ偏光板が90o回ったところに現れるので,その性質を利用して平均を取ると精度が上がる.
2: 試料の複素屈折率の決定
1. 式(3.19)を使い,Pを計算する.
2. 式(3.20)を使い, Dを計算する.
3.
![]() から,yを計算する.
から,yを計算する.
4. 式(3.30)を使い,nを求める.
5. 式(3.31)を使い,kを求める.
6. Mathematicaの様な複素数の三角関数が扱えるツールがあったら以下の手順で厳密なn,kを求めて見よ.

測 定 例
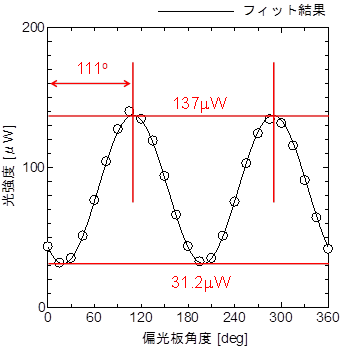
図7: 実験の結果
![]() ,
,![]() ,a=111o.
,a=111o.
ここから,射出光は図8の様な楕円偏光であることがわかる.
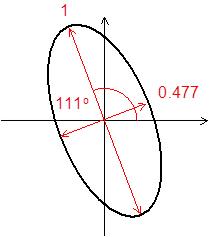
図8: 計測結果から再現された楕円偏光.
1.
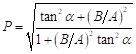 = 1.65975
= 1.65975
2.
![]() = 118.423o
= 118.423o
3.
![]() =58.9311o
=58.9311o
4.
![]() = 2.08319
= 2.08319
5.
![]() = 1.66366
= 1.66366
付 録 マクスウェル方程式と電磁波
はじめに,マクスウェル方程式(1.4)の回転を取る.
![]() (A1)
(A1)
出てきたrotBを式(1.3)で置き換えて(B=mH),
![]() (A2)
(A2)
を得る.ここで,系には自由な電荷が存在しないとしよう.するとJが0になり,整理すると
となる.一方,左辺は,ベクトル演算の恒等式![]() を利用すると,
を利用すると,
![]() (A4)
(A4)
となる.系には自由な電荷がないと仮定したから,式(1.1)よりdivD = r = 0,すなわちdivE=0である.したがって式(A3)は
と変形された.
式(A5)が電磁波を生む「波動方程式」なのだが,これ条件なしに解くことは難しい.なぜなら,この世の全ての電磁波がこの方程式の解なのだから.そこで,式(A5)を満たすと考えられるある単純な解の形を仮定して,それが式(A5)を満たすことを証明することで解の一つを見つけよう.
いま,方程式の解E(x,y,z,t)が以下の条件を満たすとする.
(1) Eはx成分しか持たない.
(2) Eは(x,y)平面内で等しい値を持つ(つまり,zのみの関数)
(3) Eのz方向の変化は調和振動的である.
(4) Eの時間変化は調和振動的である.
以上の条件を満たす関数として,
を思い浮かべることができるが,これが式(A5)の解になりうるか調べて見る.条件(1),(2)から式(A5)は以下のように簡略化される.
式(A7)に式(A6)を代入する.
![]()
![]()
つまり,wとkの間に式(A8)の関係が満たされるなら,式(A6)の関数はマクスウェル波動方程式の解であることが証明された.即ち,マクスウェル方程式を満たす電磁波のうち最も単純な形である「平面波」の存在が示されたわけである.
式(A6)を変形して見る.
ここで,定数cを![]() と定義している.t=0で時間を固定すると,Exの変化は正弦関数的である.つまり
と定義している.t=0で時間を固定すると,Exの変化は正弦関数的である.つまり
![]() (A10)
(A10)
と,電場の強弱は周期Dz=2p/k で変化している.この周期を「波長」と呼ぶ.z=0で観測を続けると,Exの大きさは正弦関数的に変化するのを感じるであろう.つまり
電場強度が毎秒振動する回数はf=w/2p で表され,これを波の周波数または振動数という.総合すると,式(A6)で表される関数は,![]() というパターンがある速度でz軸方向に進行していると見ることができる.
というパターンがある速度でz軸方向に進行していると見ることができる.![]() =constの点,たとえば電場がいちばん強い点について行くように移動すると,その移動速度は
=constの点,たとえば電場がいちばん強い点について行くように移動すると,その移動速度は![]() となることがわかる.つまり,式(A9)は,速度cで進む波を表しているという結論が導かれる.この速度cを,電磁波の位相速度と呼ぶ.真空における電磁波の位相速度は一定不変の定数
となることがわかる.つまり,式(A9)は,速度cで進む波を表しているという結論が導かれる.この速度cを,電磁波の位相速度と呼ぶ.真空における電磁波の位相速度は一定不変の定数
![]() =299
792 458 m/s (A12)
=299
792 458 m/s (A12)
で,これが光の速さとして知られている量である.
今までは電磁波の電場にのみ注目していたが,マクスウェル方程式は電場と磁場の連立方程式になっているので,電場が決まれば磁場の時間空間的振動は自動的に決まる.式(1.4)をデカルト座標で書き下すと
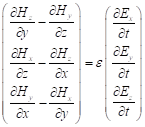 (A13)
(A13)
となるが,ここに平面波解を代入し,物理的直感として![]() を与えると
を与えると
![]() (A14)
(A14)
が得られる.これをzについて1回積分すれば,
が得られる.式(A15)から,幾つかのことがわかる.
(1) Hはy成分しか持たない.つまり,電磁波においては電場と磁場は直交している.
(2) 電場と磁場は同じ周期で振動している.即ち,電場と磁場の大きさの比率は一定である.
この,電場と磁場の大きさの比率は特性インピーダンスと呼ばれる.式(A9)と式(A15)から,特性インピーダンスは
![]() (A16)
(A16)
と,物質に固有の量であることがわかる.真空にも当然特性インピーダンスがあり,大きさは約377Wである.特性インピーダンスを理解すると,電磁波の反射,屈折などの現象を大変明快に説明することができる.