力学1(再履修)(SP)
指定教科書
 |
「講談社基礎物理学シリーズ1 力学」 副島 雄児), 杉山 忠男 (著) 教科書は必ず購入しましょう. 指定教科書の入手方法はこちら. |
関数電卓の選び方,使い方
小テストの解答と解説
過去の試験問題
履修者のみが閲覧できます.下のボックスに学籍番号を入力してください.
メールでの質問
ニュートン力学One Point Lesson
1. 1階非斉次線形微分方程式の解法
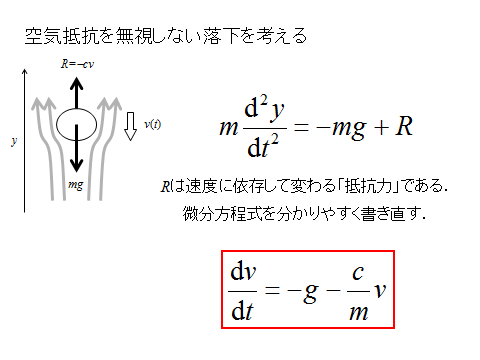
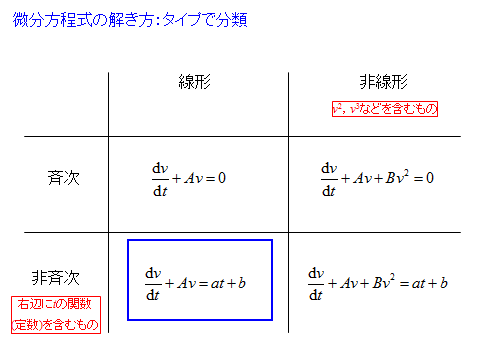

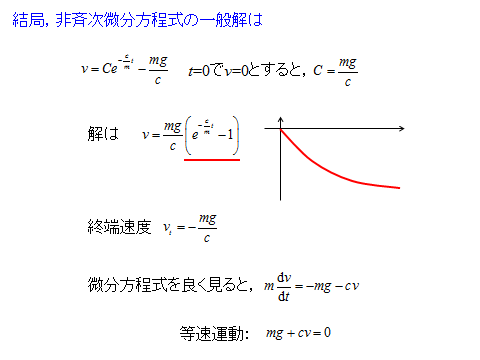
2. 物体の運動の戦略的解法フローチャート
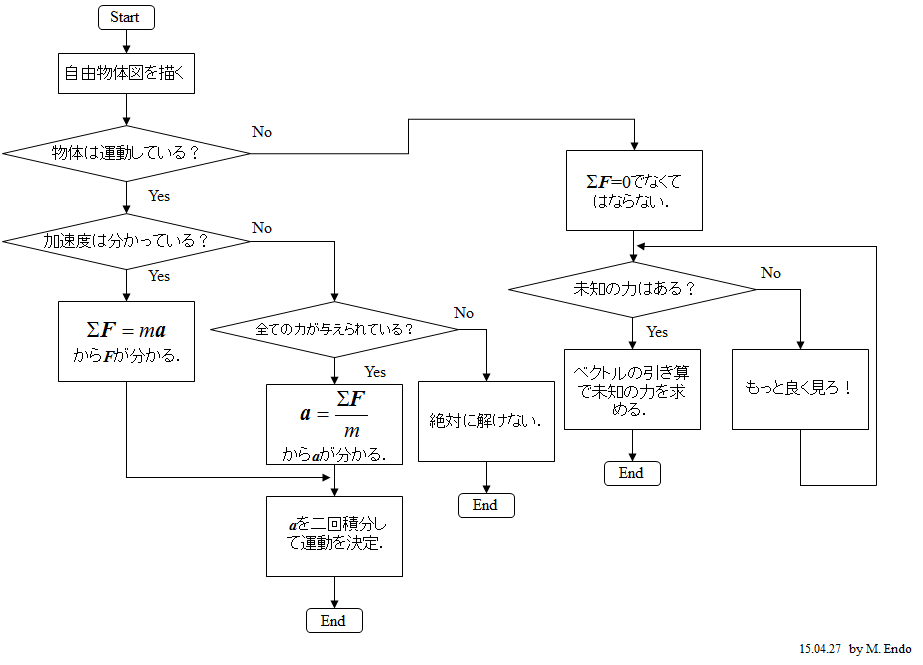
3. 力の法則
3-1. 垂直抗力の原理
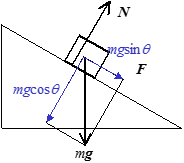
- 面に物を置くと,必ず垂直抗力が発生する.
- 垂直抗力は必ず面に垂直な方向,物体を押す力である.
- 垂直抗力の大きさは,物体を面に押しつける力(重力の場合が多い)と必ずつりあう.
3-2. ひもの原理
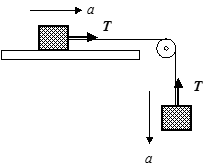
- ひもの両端には等しい張力Tが働いている.
- ひもの張力はかならずひもの方向である.
- ひもの両端につけられた物体の運動(加速度,速度,位置変化)は常に一致する.
3-3. 摩擦の法則
- 全般のルール
- 摩擦力は必ず面に水平に働く.
- 摩擦係数$\mu$が定義されており,摩擦力は$\mu$と垂直抗力$N$の積で表される.ただし,適用するときは下のルールを良く読む.
- 静止摩擦(物体が動いていないときのルール)
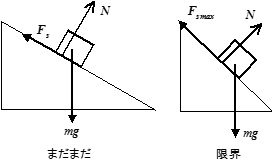
- 摩擦力$F_{\rm s}$の大きさはすぐにはわからない.そもそも値は一定でない.
- 摩擦力$F_{\rm s}$の大きさを知るには,力のつりあいを考え,面に平行,かつ物体が静止するような大きさを決める.従って物体が静止しているときは,まず力の釣り合いを求めること.
- 摩擦力$F_{\rm s}$の大きさには限界がある.最大静止摩擦力$F_{\rm smax}$は
\begin{aligned}
F_{\rm smax}=\mu_{\rm s}N
\end{aligned}
で表され,これを越えると物体は動き出す.$\mu_{\rm s}$を「静止摩擦係数」という.
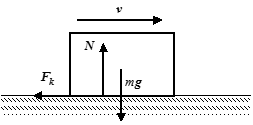
- 動摩擦(物体が動いているときのルール)
- 摩擦力$F_{\rm s}$の大きさは一定である.これは,物体の運動速度によらない.
- 摩擦力$F_{\rm k}$は
\begin{aligned}
F_{\rm k}=\mu_{\rm k}N
\end{aligned}
で表され,$F_{\rm k}$を「動摩擦係数」という.従って物体が動いているときはまず$N$を求めること.
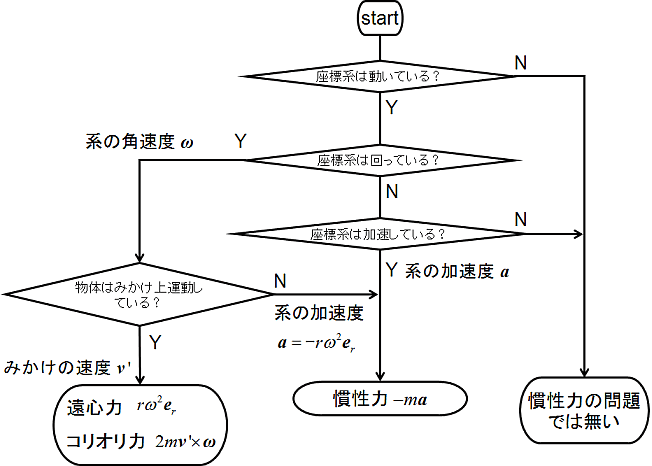
4. 慣性力フローチャート
5. 並進運動と固定軸回りの回転運動の関係
| 並進運動 | 回転運動 | ||
| $x$ | 独立変数 | $\theta$ | |
| $v=\bib{x}{t}$ | 速度$v$ | 角速度$\omega$ | $\omega=\bib{\theta}{t}$ |
| $a=\bib{v}{t}=\bib{^2x}{t^2}$ | 加速度$a$ | 角加速度$\beta$ | $\beta=\bib{\omega}{t}=\bib{^2\theta}{t^2}$ |
| $v=v_0+at$ | 等加速度運動 | $\omega=\omega_0+\beta t$ | |
| $x=x_0+v_0 t+\frac{1}{2}at^2$ | $\theta=\theta_0+\omega_0 t+\frac{1}{2}\beta t^2$ | ||
| $m$ | 質量$m$ | 慣性モーメント$I$ | $I=\iiint r^2\rd m$ |
| $F$ | 力$F$ | トルク$N$ | $N=Fr\sin\varphi$ |
| $F=ma$ | 運動の法則 | $N=I\beta$ | |
| $K=\frac{1}{2}mv^2$ | 運動エネルギー | $K=\frac{1}{2}I\omega^2$ | |
| $W=F\cdot\Delta x=\Delta K$ | 仕事-エネルギー定理 | $W=N\cdot\Delta \theta=\Delta K$ | |
| $p=mv$ | 運動量$p$ | 角運動量$L$ | $L=I\omega$ |
| $F=\bib{p}{t}$ | 運動量と運動の法則 | $N=\bib{L}{t}$ | |
| $\Delta p=F\Delta t$ | 運動量-力積定理 | $\Delta L=N\Delta t$ | |
