電磁場(SP)

世界一易しいPoisson方程式シミュレーション

1. はじめに

教科書の3章ではPoisson方程式(ポアソン方程式)の導出とその応用について学んだ．そして，「どんな複雑な問題でも数値的解法ならば必ず領域内の全ての点における電位が決定できる」ことを教えた．実際，複雑な問題(たとえば電子レンジや携帯電話など)で系の任意の点の電位，電場を求めるためのシミュレーションソフトウェアが市販されており，広く使われている．

このようなソフトウェアはもちろん非常に高度な技術を駆使して問題を解いているのだが，Poissonの方程式を数値的に解く基本原理は実は驚くほど簡単なのだ．このページでは，「世界一やさしい」を目標に，Poissonの方程式を数値的に解くシミュレーションソフトウェアについて一緒に考えてみようと思う．

2．方程式の離散化

基礎方程式は以下の形をしている．分かっているものは電荷 $\begin{displaymath} \rho \end{displaymath}$ の分布で，知りたいものは系の全ての点における $\begin{displaymath} \phi \end{displaymath}$ だ．

$\begin{displaymath} \nabla^2 \phi = -\frac{\rho}{\varepsilon _0} \end{displaymath}$ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(1)

いま，話を簡単にするために系は二次元とする．つまり電位は（x,y）の関数でz方向には変化がないものとする．現実の世界ではこのような条件はありえないが，近似的には長い棒状の電荷や導体が存在する系の，棒に垂直な断面の電位がこの問題に相当する．すると式(1)は以下のように書き下すことが出来る．もちろん，僅かな努力の上積みで以下の議論は容易に三次元に拡張できる．

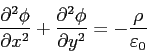$\begin{displaymath} \frac{\partial^2\phi}{\partial x^2} + \frac{\partial^2\phi}{\partial y^2} =-\frac{\rho}{\varepsilon _0} \end{displaymath}$ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(2)

続いて，この方程式を離散化しよう． $d\phi/dx$ の定義は

$\begin{displaymath} \lim_{\Delta x\rightarrow0} \frac{\phi(x, y)-\phi(x-\Delta x, y)}{\Delta x} \end{displaymath}$ 　　　　　　　　　　　　　　　　　　　　　　　　(3)

だ．ここで，差分を取るときに $\begin{displaymath} \phi(x, y) \end{displaymath}$ と $x$ が小さい隣の点との差を取った．これを「後方差分」と呼ぶ．逆に， $x$ が大きい点との差分を取ると「前方差分」になるのだが，今は細かいことは気にしない．どうせ， $\Delta x$ は非常に小さいのだから．「方程式の離散化」とは，この $\Delta x$ が有限の大きさを持つとして，微分を差分に置き換えて計算を行うことに相当する．

次に， $d^2\phi/dx^2$ を考えよう． $d^2\phi/dx^2$ は $d\phi/dx$ の微分なのだから，以下のように書き下すことが出来るだろう．

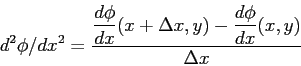
$\begin{displaymath} d^2\phi/dx^2=\frac{\displaystyle{\frac{d\phi}{dx}}(x+\Delta x, y)-\displaystyle{\frac{d\phi}{dx}}(x, y)}{\Delta x} \end{displaymath}$

　　　　　　　 $\begin{displaymath} =\left[\frac{\phi(x+\Delta x, y)-\phi(x, y)}{\Delta x}-\frac{\phi(x, y)-\phi(x-\Delta x, y)}{\Delta x}\right]/{\Delta x} \end{displaymath}$ 　
　　　　　　　 $\begin{displaymath} =\frac{\phi(x+\Delta x, y)+\phi(x-\Delta x, y)-2\phi(x, y)}{\Delta x^2} \end{displaymath}$ 　　　　　　(4)

ここでちょっとズルをして，今度は前方前方差分を取った．すると， $d^2\phi/dx^2$ は， $\begin{displaymath} \phi(x, y) \end{displaymath}$ とその上流，下流の両隣の2点の値で表されることがわかる．

次に系を二次元のグリッドに区切り，それぞれの点に以下のような番号を付ける．今の例では，系は8×7=56個の点で代表されることになる．

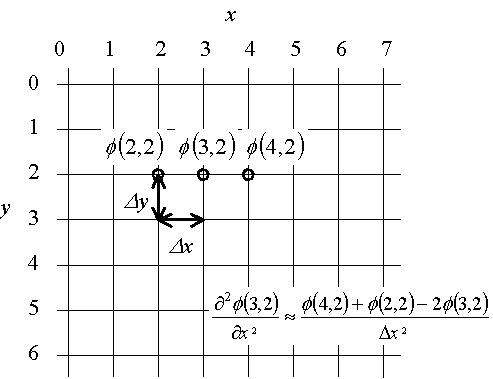
図1: 系を二次元のグリッドに分割，インデックスを付ける

すると式(4)は $(i, j)$ を使って式(5)の様に書ける．

$\begin{displaymath} \frac{d^2\phi(i, j)}{dx^2}=\frac{\phi(i+1, j)+\phi(i-1, j)-2\phi(i, j)}{\Delta x^2} \end{displaymath}$ 　　　　　　　　　(5)

いま，ある点 $(i, j)$ の電位のみがわからず，まわりの電位は分かっているとしよう．すると $\phi(i, j)$ はPoissonの方程式(2)を使って簡単に求めることが出来ることに気づく．

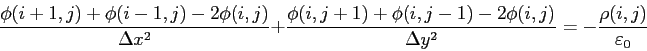
$\begin{displaymath} \frac{\phi(i+1, j)+\phi(i-1, j)-2\phi(i, j)}{\Delta x^2}+ ... ...-2\phi(i, j)}{\Delta y^2} = -\frac{\rho(i, j)}{\varepsilon _0} \end{displaymath}$

ここで，話を簡単にするために $\Delta x =\Delta y = \Delta$ としよう．すると，整理して

$\begin{displaymath} \phi(i, j) = \frac{1}{4} \left[\frac{\Delta ^2\rho(i, j)}{\v... ...0}+\phi(i+1, j)+\phi(i-1, j)+ \phi(i, j+1)+\phi(i, j-1)\right] \end{displaymath}$ 　　(6)

を得る．実際には点 $(i, j)$ のまわりの電位も確定していないのだから，このように一発で解を求めることは出来ない．しかし，何らかの方法で，全ての点で $\phi(i, j)$ が正しく求まるとすれば，それは全ての点で式(6)が満たされていることと等価である．端から書き下していくと，

$\begin{displaymath} \phi(1, 1) = \frac{1}{4} \left[\frac{\Delta ^2\rho(1, 1)}{\varepsilon _0}+\phi(2, 1)+\phi(0, 1)+ \phi(1, 2)+\phi(1, 0)\right] \end{displaymath}$
$\begin{displaymath} \phi(2, 1) = \frac{1}{4} \left[\frac{\Delta ^2\rho(2, 1)}{\varepsilon _0}+\phi(3, 1)+\phi(1, 1)+ \phi(2, 2)+\phi(2, 0)\right] \end{displaymath}$
$\begin{displaymath} \phi(3, 1) = \frac{1}{4} \left[\frac{\Delta ^2\rho(3, 1)}{\varepsilon _0}+\phi(4, 1)+\phi(2, 1)+ \phi(3, 2)+\phi(3, 0)\right] \end{displaymath}$
　　　　　　　　　　　　　　　　　　　　　　　　　　　　．
　　　　　　　　　　　　　　　　　　　　　　　　　　　　．
　　　　　　　　　　　　　　　　　　　　　　　　　　　　．

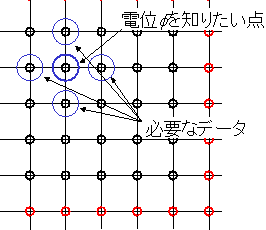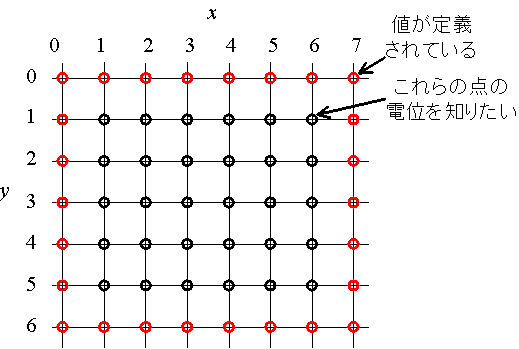
図2: 境界条件を定めたセル

いま，問題は8×7個の未知数のある連立方程式になることに気づく．しかし，厳密に言うと領域の一番端，例えば $i=0$ の電位は，その外側の電位が定義されないので式(6)の方法では決定できない．実は，これがPoissonの方程式における「境界条件」に当たる．つまり，領域の一番端の電位はあらかじめ決めておかないといけないのだ．これで，解くべき問題は(8-2)×(7-2)=30個の未知数がある連立方程式になった．

上の式を見て，電荷が無い場合のPoissonの方程式(Laplaceの方程式)の意味するところは，「ある場所の電位は，近傍の電位の平均値に等しい」と言っているに過ぎないことに気がついただろうか．

3．方程式の解き方

上で導いたような大規模な連立方程式の解法にはそれだけで本が書けるような奥深い学問がある．しかしここではそういった理屈は全てすっ飛ばして，この問題を楽に解く方法を考える．

まず，領域内の，図2上で黒丸で表された点の電位を全て0に定義．そして， $(1, 1)$ から順番に式(6)を解いて，電位の値を書き換えていく．暫定的に全ての点の電位が決まっているのだから，とりあえず全ての点の電位は計算可能だ．ここで，たとえば $\phi(5, 5)$ を計算するときに， $\phi(4, 5)$ の電位と $\phi(6, 5)$ の電位が必要になるが，前者は既に一度計算を終えて更新された値が入っており，後者はまだ計算が済んでいないので0が入っている．不公平ではないかと思うかも知れないが，細かいことは気にしない．

こうして，全ての点の $\phi$ が計算された．いくつかの点において， $\phi$ は0ではないある値になった．が，これらの $\phi$ は式(6)を同時には満たしていない．なぜなら，ある点の電位を計算するのに使った両隣の電位は暫定的に決めた電位だから．

では，同じ手続きをもう一度くり返そう．すると，全ての点において $\phi$ は前回のループとは違う値になる．実は，2回目のループを終えると，各点の電位は1回目よりも正解に近くなる．ではもう一度くり返そう．3回目のループを終えると，電位の分布はならされて，更に正解に近くなる．この手続きをくり返して行くと，前のループの $\phi(i, j)$ と現ループで計算した $\phi(i, j)$ がほとんど変わらなくなっていく．

手続きを無限にくり返すと，何度くり返しても $\phi(i, j)$ は全く変化しなくなる．このとき，全ての点において，式(6)が同時に満たされていることに気がつくだろうか．つまり，連立方程式が解けた事になる．この解法は「ガウス=ザイデル法」と呼ばれているもので，歴史と伝統のある多元連立方程式の解法なのだ．

4．具体的なプログラム

図3: 例題：正方形の領域におかれた円形電荷

それでは，何か一つ問題を解いてみよう．問題は，図3のように，1辺1mの正方形の領域の中に半径5cmの正電荷が存在するとする．領域端の電位は0で，電荷密度は $1.0\times 10^{-8}$ [C/m $^2$ ]とする．「この系における電位分布，電場分布を求めよ」と言うのが問題．プログラミング言語として，広く使われているC(++)を選ぼう．プログラムの流れは以下のようになる．

解くべき解答を入れる行列phi，電荷密度を入れる配列rhoを定義．ここで配列数をN×Nとする．
phi，rhoを領域全体にわたりクリア．その後問題定義に従ってrhoを配置．
領域端を除く範囲で 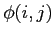$\phi(i, j)$ の値を式(6)に従って計算．
3の計算によってphiの値は変化したか？　Yes-> 3. No-> 5．
計算終了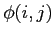． $\phi(i, j)$ の値から電場を計算する．
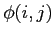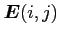$\phi(i, j)$ ， ${\mbox{\boldmath$E$}}(i, j)$ を出力．

以下，順番に見ていこう．

4-1. 配列定義，変数の宣言

/*-----------------------------------------------------------------------------
     Program Poisson.c
     二次元Poisson方程式シミュレーション
-----------------------------------------------------------------------------*/
#include <stdio.h>
#include <math.h>


/* マクロ定義 ---------------------------------------------------------------*/
#define N   100

/* メインルーチン -----------------------------------------------------------*/
int main(void) {

    const double X     = 1.0       ;     /* 計算領域の大きさ                 */
    const double e0    = 8.85e-12  ;     /* 真空の誘電率                     */
    const int    center= (int)(N/2);     /* 中心の座標                       */
    const double delta = X/N       ;     /* δ                               */
    const double Conv  = 1.0e-6    ;     /* 収束と判定する前回ループとの差   */

    double phi[N][N]               ;     /* 計算するべき電位                 */
    double rho[N][N]               ;     /* 電荷密度                         */
    double MaxPhi                  ;     /* 最大電位                         */
    double MaxErr                  ;     /* 最大のエラー                     */
    double CurErr                  ;     /* 現在のエラー                     */
    double Prev_phi                ;     /* 前のループのφ                   */
    double Ex, Ey                  ;     /* 電場                             */
    int    i, j                    ;
    int    loop                    ;     /* 繰り返しカウンタ                 */
    FILE   *f                      ;     /* ファイルハンドラ                 */

C言語では，数値計算を行って結果を出力するプログラムでははじめに<stdio.h>と<math.h>ヘッダを使うことを宣言する．これはおまじないと思ってもらって良い．続いて配列の大きさNを宣言するが，これは「プリプロセッサによる定義」と呼ばれる方法である．C言語では，配列の大きさをプログラム内部で自由に変えることが出来ないので，プログラム本体の記述に入る前に「以降，Nが出たらこれを100と置き換えよ」と宣言する．

続いて，メインルーチン先頭で，プログラム中で使用する変数を宣言する．const宣言とは，始めに定義した値が変わらない様な数値に対して使う．const宣言された変数に値を代入しようとするとエラーになるので，うっかりミスを防ぐことができる．

4-2. 配列phi，rhoのクリア，電荷密度を定義する

    /* phi(i, j)，rho(i, j)をクリアする */
    for (i = 0; i < N; i++) {
        for (j = 0; j < N; j++) {
            phi[i][j] = rho[i][j] = 0.0;
        }
    }

    /* 電荷を置く */
    for (i = 0; i < N; i++) {
        for (j = 0; j < N; j++) {
            if(((center-i)*(center-i)+(center-j)*(center-j))*delta*delta<0.05*0.05) {
                rho[i][j] = 1.0e-8;
            }
        }
    }

典型的な，二次元配列に対するループ処理．特に説明の必要は無いと思う．

4-3, 4. 繰り返し計算，収束の判定

    /* 繰り返し計算 */
    loop   = 0;         /* 別に無くても良いのだが，目安としてループをカウントする．              */
    MaxPhi = 1.0e-10;   /* 系内の最大の電位を入れる変数．ある有限の値を入れておく(ゼロ割り防止)．*/

    do {
        if(!(loop%1000)) printf("%05d  %e\n", loop, MaxPhi); /* 10000ループ毎に経過表示 */
        MaxErr = CurErr = 0.0;
        for (i = 1; i < N-1; i++) {      /* 領域端を除く全ての点をループ                */
            for (j = 1; j < N-1; j++) {  /*                                             */
                Prev_phi = phi[i][j];    /* 前回ループのphiをPrev_phiにいれておいて，   */
                phi[i][j] = 0.25*(rho[i][j]*delta*delta/e0+phi[i+1][j]+phi[i-1][j]+phi[i][j+1]+phi[i][j-1]);
                                         /* Poissonの方程式でphiを計算する．            */
                if (MaxPhi < fabs(phi[i][j])) MaxPhi = phi[i][j];
                                         /* 電位最大が更新されたらMaxPhiを書き換え      */
                CurErr = (fabs(phi[i][j] - Prev_phi))/MaxPhi;
                                         /* 前回ループと新しい答えの差を，MaxPhiで規格化*/
                if (MaxErr < CurErr) MaxErr = CurErr;
                                         /* 誤差の最大を常にMaxErrに持つようにする      */
            }
        }
        loop++;
    } while (MaxErr>Conv);               /* 領域全ての点の誤差がConvを下回ったらおしまい*/

ここがプログラムの本体．たったこれだけだ．しかも，記述のほとんどはループ制御，収束判定に費やされていて，実際にPoissonの方程式を解いているのは

phi[i][j] = 0.25*(rho[i][j]*delta*delta/e0+phi[i+1][j]+phi[i-1][j]+phi[i][j+1]+phi[i][j-1]);

この部分だけ．各行で何をやっているのか，詳しいコメントを付けておいたので参照してほしい．

4-5, 6. 電場，電位の出力

    /* ポテンシャル出力 */
    f = fopen("Phi.avd", "wt");
    for (i = 0; i < N; i++) {
        for (j = 0; j < N; j++) {
            fprintf(f, "%e %e %e\n", delta*i, delta*j, phi[i][j]);
        }
    }
    fclose(f);

    f = fopen("Phi.gdw", "wt");
    for (i = 0; i < N; i++) {
        fprintf(f, "%e %e\n", delta*i, phi[i][center]);
    }
    fclose(f);

    /* 電場出力 */
    f = fopen("Electric.avd", "wt");
    for (i = 1; i < N-1; i++) {
        for (j = 1; j < N-1; j++) {
            Ex = -(phi[i+1][j]-phi[i-1][j])/(2.0*delta);
            Ey = -(phi[i][j+1]-phi[i][j-1])/(2.0*delta);
            fprintf(f, "%e %e %e %e %e\n", delta*i, delta*j,  sqrt(Ex*Ex+Ey*Ey), Ex, Ey);
        }
    }
    fclose(f);

    f = fopen("Electric.gdw", "wt");
    for (i = 0; i < N; i++) {
        Ex = -(phi[i+1][center]-phi[i-1][center])/(2.0*delta);
        fprintf(f, "%e %e\n", delta*i, Ex);
    }
    fclose(f);

    return 0;
}

最後に，電位と電場を出力する．お気づきのように，データを出力するルーチンの方が肝心のPoisson方程式ソルバより長い．実はこう言うことは普通にあることで，プログラマにとって苦労が多いのは計算させる中身より入力／出力だったりする．市販の高価なシミュレーションソフトの価格の大半は，誰でも使えるユーザーインターフェース構築につぎ込まれていると言っても良いだろう．

ダウンロード可能なソースコードはこちら．

電場，電位の出力ファイルについて

このページではPoisson方程式の解き方に主眼を置いているので上の出力ルーチンが何をやっているのかは詳しく解説しない．簡単に説明すると，

ファイル名	データ内容	表記方法
Phi.avd	電位分布の二次元データ	x, y, φ(x, y)
Phi.gdw	y=centerのライン上，電位分布の一次元データ	x, φ(x, center)
Electric.avd	電場分布の二次元データ	x, y, E(x, y), Ex(x, y), Ey(x, y)
Electric.gdw	y=centerのライン上，電場(Ex)分布の一次元データ	x, Ex(x, y)

を出力する処理をやっている．電場の計算については，各座標点において

${\mbox{\boldmath$E$}}= -{\rm grad}\phi$ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(7)

を離散化した計算

$\begin{displaymath} E_x(i, j) = \frac{\phi(i+1, j)-\phi(i-1, j)}{2\delta} \end{displaymath}$ 　　　　　　　　　　　　　　(8)
$\begin{displaymath} E_y(i, j) = \frac{\phi(i, j+1)-\phi(i, j-1)}{2\delta} \end{displaymath}$ 　　　　　　　　　　　　　　(9)

を行って出力している．ここで差分は，偏りが出ないように前方と後方の二点を使った「中心差分」を取っている．

二次元データを表示するのに便利なフリーソフトとしてAV似非を紹介しよう．上のデータ表記法はそのままAV似非で表示可能なように作っている．出力例を下に示す．

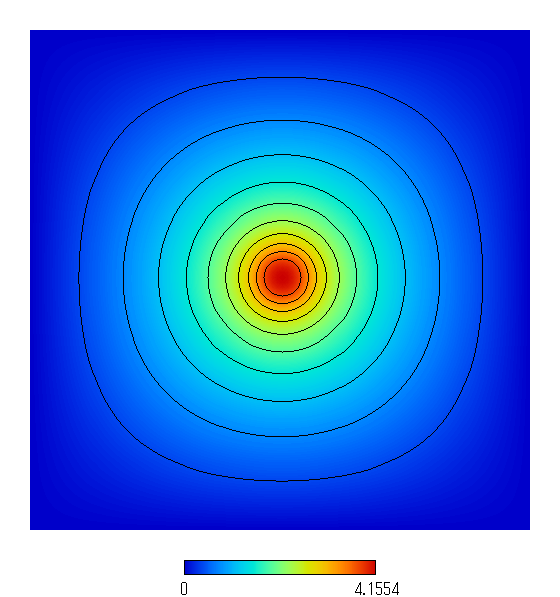
図4(a): 計算された電位分布の等高線表示(AV似非使用)

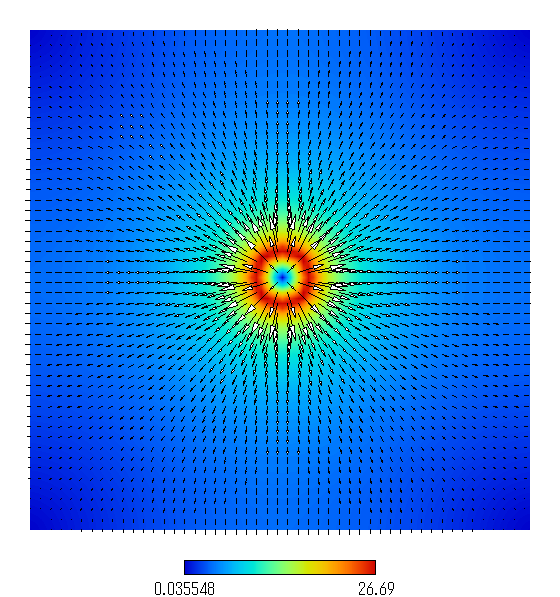
図4(b): 計算された電場分布の二次元ベクトル表示(AV似非使用)

一次元のデータについては紹介する必要も無いだろうが，私は長年Ngraphというシェアウェアを愛用している．

検算

最後に，計算結果を検算してみよう．上の問題は「電荷円盤中央から半径0.5mの位置における電位を0と定義」すれば，解析的に解ける．途中経過は省略して答だけ述べると，電荷円盤の半径を中心とした極座標で，電荷半径を $r_0$ ，電位0の位置の半径を $a$ として

$r<r_0$ ：

$\begin{displaymath} E_r(r) = \frac{r\rho}{2 \varepsilon _0} \end{displaymath}$
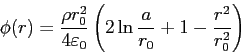
$\begin{displaymath} \phi(r) = \frac{\rho r_0^2}{4 \varepsilon _0}\left(2 \ln\frac{a}{r_0}+1-\frac{r^2}{r_0^2}\right) \end{displaymath}$

$r>r_0$ ：

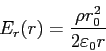
$\begin{displaymath} E_r(r) = \frac{\rho r_0^2}{2 \varepsilon _0 r} \end{displaymath}$
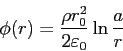
$\begin{displaymath} \phi(r) = \frac{\rho r_0^2}{2 \varepsilon _0}\ln\frac{a}{r} \end{displaymath}$

となる．具体的な数値を代入して解き，上述のPhi.gdw，Electric.gdw出力ファイルと比べてみよう．

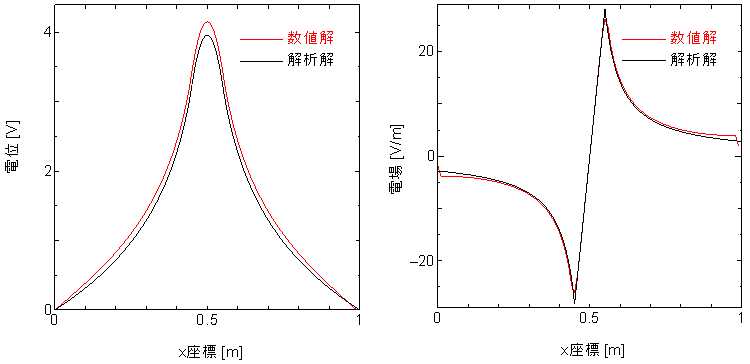
図5: 電場，電位のシミュレーションによる数値解と解析解の比較

どちらも，良く一致していると言って良いのでは無いだろうか．誤差の原因は幾つか考えられるが，大きな原因として，電荷円盤の定義範囲が(10×10)と小さな領域であったための離散化誤差，そしてシミュレーションでは電位0に定義されたのは1辺1mの正方形のへりで円形の境界では無いことが挙げられる．

5．応用問題

次に，応用問題として系に導体が置かれた場合の計算方法について述べる．導体が接地されていると仮定した場合，計算は簡単だ．phi[i][j]を更新するときに，「導体があるところは常に0」となるようなプログラムを組んでやればよい．例題として以下の系を考えよう．

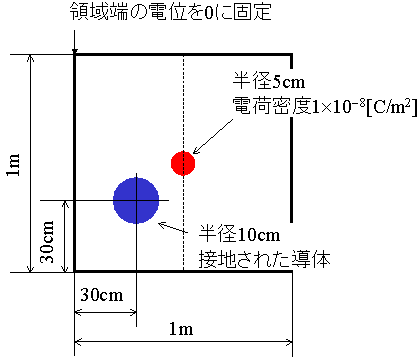
図6: 例題(2) - 接地された導体円盤と電荷円盤の系

プログラムの変更も簡単で，金属のある位置を示す配列metal[N][N]を用意して，金属のあるところは1とする．そして，Poissonの方程式を解くときに，metal=1の座標は飛ばすようにすればよいだけのことだ．

※後の拡張を考慮して，metal[N][N]は実数配列としている．

    /* 繰り返し計算 */
    loop   = 0;         /* 別に無くても良いのだが，目安としてループをカウントする．              */
    MaxPhi = 1.0e-10;   /* 系内の最大の電位を入れる変数．ある有限の値を入れておく(ゼロ割り防止)．*/

    do {
        if(!(loop%1000)) printf("%05d  %e\n", loop, MaxPhi); /* 10000ループ毎に経過表示 */
        MaxErr = CurErr = 0.0;
        for (i = 1; i < N-1; i++) {      /* 領域端を除く全ての点をループ                */
            for (j = 1; j < N-1; j++) {  /*                                             */
                if(metal[i][j]==0) {
                    Prev_phi = phi[i][j];    /* 前回ループのphiをPrev_phiにいれておいて，   */
                    phi[i][j] = 0.25*(rho[i][j]*delta*delta/e0+phi[i+1][j]+phi[i-1][j]+phi[i][j+1]+phi[i][j-1]);
                                         /* Poissonの方程式でphiを計算する．            */
                    if (MaxPhi < fabs(phi[i][j])) MaxPhi = phi[i][j];
                                         /* 電位最大が更新されたらMaxPhiを書き換え      */
                    CurErr = (fabs(phi[i][j] - Prev_phi))/MaxPhi;
                                         /* 前回ループと新しい答えの差を，MaxPhiで規格化*/
                    if (MaxErr < CurErr) MaxErr = CurErr;
                }                        /* 誤差の最大を常にMaxErrに持つようにする      */
            }
        }
        loop++;
    } while (MaxErr>Conv);               /* 領域全ての点の誤差がConvを下回ったらおしまい*/

修正されたソースコードはこちら．

計算結果を以下に示す．導体円盤が置かれたことによって期待される通りの結果が得られている．

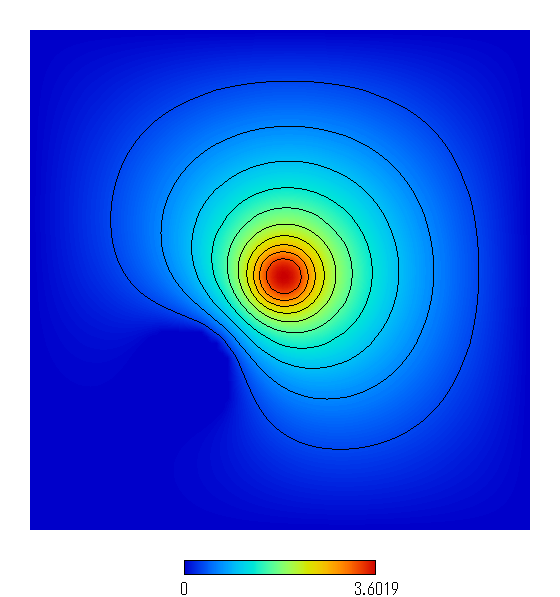
図7(a): 計算された電位分布の等高線表示(AV似非使用)．導体に等電位面が「押される」様子が分かる．

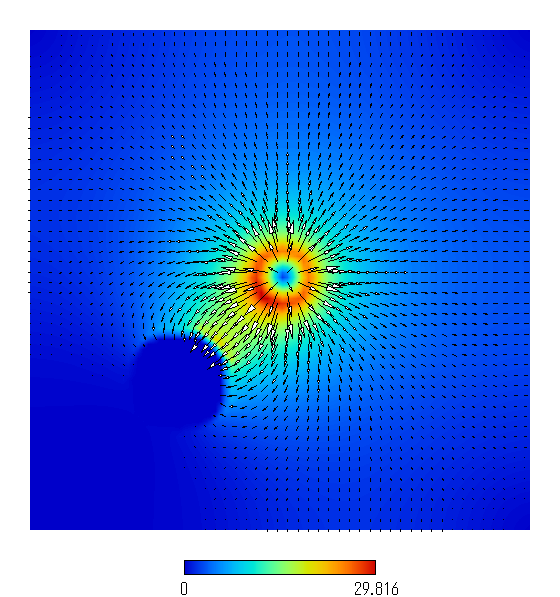
図7(b): 計算された電場分布の等高線表示(AV似非使用)．導体からは電気力線は垂直に発する．

6．まとめ

これで，説明はおしまい．Poissonの方程式は本質的にはたった1行の計算式で表せること，プログラムの大部分は計算をコントロールすることと，入出力の処理に費やされることを理解してもらえただろうか．

ここから先は君たち自身で，他の問題を解くためにソースコードを書き換えたり，接地されていない導体の扱いを考えたり，電場の法線成分固定を境界条件とする問題の解き方を考えたり，系を三次元に拡張したりと自由に楽しんで欲しい．