A1: この問題は，半分は電磁気学だが，半分は「フェルミ推定」という物理学者にとって必須のスキルの練習問題である．ポイントは，与えられた条件を「常識的に正しい」数値に置き換える能力である．その意味では，一番困難な，はじめの「問の設定を2個の点電荷間のクーロン力に置き換える」ステップが問題文で与えられている．これはサービスである．では続けよう．
問題は，「2個の点電荷がある距離$d$未満に近づいたとき，クーロン力が重力を上回る条件」と読み替えられる(図1)．

図1: フェルミ推定により置き換えられた問題

はじめに，紙にかかる重力を計算する．紙の大きさは$1$cm$\times1$cm，重さは標準的なA4版のコピー用紙が$4$gと言われているから，面積で割り$6.3$mgとなる．したがって重力の大きさ$mg$は$6.2\times10^{-5}$Nと出た．

一方，クーロン力の大きさは \begin{eqnarray} \label{eq1} F = \frac{1}{4 \pi \varepsilon_0}\frac{q^2}{d^2} \end{eqnarray} だが，ここで曖昧なのが$d$である．直感的にも，YouTubeの映像でも，この距離は$1$cmのオーダーである．$1$cmを使おう． $d=0.01$m，$F$=$6.2\times10^{-5}$Nを代入し，$q=8.9\times10^{-10}$Cを得る．答はオーダーで解答すべきで，「約$1$nC」である． よほど変な推定をしない限り，この値の$1/10$から$10$倍の範囲に収まるはずである．計算の根拠が正しい限りはどんな値でも正解とする．

Q1の解答で，紙片の重さを根拠なしに決定しているレポートが相当数あった．これらはフェルミ推定の観点から不正解とする．

A2: この問題は電磁気学以前に，ベクトルの基本的数学がわかっているかどうかを問うものである． 本当はこういう問題は好きではないが，例年，レポートの出来が悪いので，まずは基本を勉強しなさい，という私からのメッセージである．ちなみに正解は「電磁場」の教科書ではなく，2年生の「電磁気学１」の教科書を見ると載っている． \begin{eqnarray} \label{eq2} \vE = \frac{q}{4 \pi \varepsilon_0 R^3} \left( \begin{matrix} x-X\\ y-Y\\ z \end{matrix} \right) \end{eqnarray}

なお，本問は$R$を使わない解答は減点とする．物理学の数式には美しさを求めたい．

配点は2問正解をA，1問正解をBとして，部分点を考慮して総合的に評価した．

今回の課題は，あまり考えずにその場の勢いで出してしまったのであまり良い問題ではなかった．正直に解いていこう．

極座標のポアソンの方程式は \begin{eqnarray} \label{eq3} \nabla^2 \phi &=& -\frac{\rho}{\varepsilon_0} \nonumber \\ \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2 \frac{\partial \phi}{\partial r}\right)+\frac{1}{r^2\sin\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\frac{\partial \phi}{\partial \theta}\right)+\frac{1}{r^2\sin^2\theta}\frac{\partial^2\phi}{\partial \varphi^2}&=& -\frac{\rho}{\varepsilon_0} \end{eqnarray} だが，系の対称性から$\theta$，$\varphi$の微分はすべて消え， \begin{eqnarray} \label{eq4} \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2 \frac{\partial \phi}{\partial r}\right)&=& -\frac{\rho}{\varepsilon_0} \end{eqnarray} を得る．球表面には面電荷があるため，計算する領域を球の外側，球の内側に分ける．どちらも領域内に電荷はないから，ポアソンの方程式はラプラスの方程式となる．積分は簡単で(教科書p91)， \begin{eqnarray} \label{eq5} \rm{\bf 球外側：}\phi &=& \frac{C_1}{r}+C_2\\ \label{eq6} \rm{\bf 球内側：}\phi &=& \frac{C_3}{r}+C_4 \end{eqnarray} ($C_1, C_2, C_3, C_4$は定数)を得た．

次に4つの積分定数を決定する．まず，$r\rightarrow\infty$で$\phi=0$だから，$C_2=0$．次に，球の内側に電荷は無いから，$r\rightarrow 0$で$\phi$は有限の大きさを持つ必要がある．したがって$C_3=0$． しかし，これだけでは$C_1$と$C_4$を決定することができない．

ポアソンの方程式は，2か所の独立した境界で値がわかっていないと電位が決定できない(教科書p88)．境界値でわかっているべき物理量は電位$\phi$か，電位の微分の法線成分，すなわち領域端の電場(の法線成分)である．外側の領域の一番内側，球表面の電場は，導体の静電平衡の定理4から， \begin{eqnarray} \label{eq7} D &=& \frac{Q}{4 \pi a^2} \end{eqnarray} とただちに求められる．これを境界条件に使えば， \begin{eqnarray} E(a) &=& \frac{Q}{4 \pi \varepsilon_0 a^2} \nonumber \\ -\frac{\rd \phi}{\rd r} &=& E(r) = \frac{C_1}{r^2} \end{eqnarray} $r = a$にて両者を比較し，$\displaystyle C_1 = \frac{Q}{4 \pi \varepsilon_0} $を得る．すなわち球の外側で \begin{eqnarray} r > 0 : \phi(r) &=& \frac{Q}{4 \pi \varepsilon_0 r} \end{eqnarray} と決定された．

球内側の電位は式(\ref{eq6})から定数で，それは球表面の電位と等しくなくてはいけない．したがって \begin{eqnarray} r \leq 0 : \phi(r) &=& \frac{Q}{4 \pi \varepsilon_0 a} \end{eqnarray} と決定された．

とまあ，これが模範解答なのだが，球外側の領域の境界条件を見出すのに，導体の静電平衡の定理(すなわちガウスの法則)を使うのは，問題として美しくない．あまり考えずに出題したツケが回った． 今回は，

• ポアソンの方程式を正しく解いている(式(5)，式(6))
• 答が正しい

解答はA評価としましょう．球外側の電位を決定するため，電場が$\displaystyle \frac{Q}{4\pi\varepsilon_0 r^2}$であることを使ってもよし．部分点は，

• 内部の電位の計算に一様電荷分布の式を適用しているが，結果的に答は合っているもの：B
• 答えが間違っているもの：C

今回の課題は，教科書にそのまま載っているのでラクショー．あとは，教科書に書いてあることが理解できるかどうか．

$\Phi_{12}$は，ループ2の電流がつくる磁場をループ1の範囲で面積分することで得る．ループ2が作る磁場のうち，ループ1の内部にあるものを$\vB_{12}$とすると，

$\vB=\rot \vA$とストークスの定理を使い，

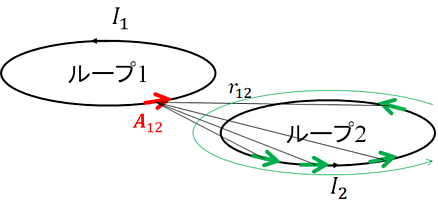
式(\ref{A3-2})を式(\ref{A3-1})に代入すれば

を得る．この積分はループ1，ループ2に対して対称であることに注意しよう．すなわち，ループ1の電流がループ2の中に作る磁束を計算しても同じ結果を得る．したがって$\displaystyle \frac{\Phi_{12}}{I_2}=\frac{\Phi_{21}}{I_1}$が成立することが示された．

採点基準は

• 図が描いてあること
• 変数を定義していること