図1: レーザーの構成概念図

図1はレーザーの構成概念図である．レーザーを構成する主な要素は

• レーザー媒質
• レーザー媒質を励起する手段
• 光共振器

で，そのどれもが重要な研究対象となっている．そして，私が大学で研究を始めてからの研究テーマの柱の一つが，「光共振器の研究」である．

光共振器とは，言ってしまえば2枚の鏡である．正確に対向した2枚の鏡は，レーザー媒質からの自然放出をフィードバックして，誘導放出を引き起こし，増幅させ，最後には発振に至らしめる．極めて単純ながら，この仕組みが1964年のノーベル物理学賞の受賞対象となっている．

世界初の光共振器は，レーザー媒質であるルビーに直接銀を蒸着した，たいそう原始的なものであった．そして，その後すぐに光共振器の理論と設計の重要性が認識され，「光共振器の理論」がレーザー研究の一つのジャンルとして確立する．

2枚のミラーが単純な球面であるとき，光共振器に成立するモードは「エルミート・ガウス関数」であることが知られてる．エルミート・ガウス関数は，Maxwellの方程式を，\(z\)軸近傍に存在する振動数\(\omega\)の波動解という前提で解いた「エルミート・ガウスビーム」

\begin{align} E(x,y,z)=&E_0\frac{w_0}{w(z)}H_m\left(\sqrt{2} \frac{x}{w(z)}\right)H_n\left(\sqrt{2} \frac{y}{w(z)}\right)\nonumber\\ &\times \exp\left[-\frac{x^2+y^2}{w^2(z)}-\frac{ik(x^2+y^2)}{2R(z)}-ikz+i(m+n+1)\phi(z)\right]\\ w(z)=&w_0\left[1+\left(\frac{z}{z_0}\right)^2\right]^{1/2}　{\rm (ビーム半径)}\\ R(z)=&\frac{1}{z}\left(z^2+z_0^2\right)　{\rm (波面曲率)}\\ \phi(z)=&\tan^{-1}\frac{z}{z_0}　{\rm (Goui位相)}\\ z_0=&\frac{\pi w_0^2}{\lambda}　{\rm (Rayleigh長)} \end{align}

\(k=\omega/c\)	電磁波の波数
\(\lambda=2\pi/k\)	電磁波の波長
\(w_0\)	ビームウェイスト(任意の定数)

を，法線が\(z\)軸に平行な2枚の球面鏡で閉じ込めたものである．

曲率半径\(R_1\)，\(R_2\)の2枚の球面鏡を距離\(l\)だけ離して対向させて置いたたとき，上述のエルミート・ガウスビームの波面曲率とミラーの曲率半径が一致すれば，ミラー面上の反射は時間反転となり，2枚のミラー間には安定な電磁場分布，すなわち共振モードが成立する．このような条件を満たす2枚のミラーの位置を，\(R_1\)，\(R_2\)および\(z_0\)で表すと以下のようになる．

\begin{align} \label{z1} z_1=\frac{R_1}{2}\pm \frac{1}{2}\sqrt{R_1^2-4 z_0^2}\\ \label{z2} z_2=\frac{R_2}{2}\pm \frac{1}{2}\sqrt{R_2^2-4 z_0^2}\\ \end{align}

ここで，\(z_2-z_1=l\)が成立する．

実際には，はじめに2枚のミラーが距離\(l\)だけ離れて置かれたとき，そこに成立するエルミート・ガウスモードが知りたい場合が多い．この場合未知数はビームウェイストの大きさとその位置である．

与えられたミラー曲率およびミラー間距離から\(z_0\)を求める式は，式\eqref{z1}，式\eqref{z2}を\(z_0\)について解き，以下のように与えられる．

\begin{align} z_0^2=\frac{l(-R_1-l)(R_2-l)(R_2-R_1-l)}{(R_2-R_1-2l)^2} \end{align}

\(z_0\)が決まれば式\eqref{z1}，式\eqref{z2}を用いて\(z\)軸の原点の位置が求められる．

上述の光共振器の理論は，解析的に解くことができる微分方程式の解である．しかし，ミラーの形状が複雑になると，解析計算(紙と鉛筆)では解が得られない．ちょうどこのころ実用的になったデジタルコンピューターが直ちに光共振器の理論解析に使われた．記念碑的論文は1961年のFoxとLiによるものである．

A. G. Fox and T. Li. “Resonant modes in a maser interferometer”, BBell Syst. Tech. J. 40, 453 (1961)

彼等は，現代の水準からすれば電卓ほどの能力のコンピューターを使い，任意の光共振器に成立する共振モードを数値計算する方法を確立した．FoxとLiの光共振器シミュレーションは，Fresnel-Kirchhoff回折積分を基礎としている．

図2: 近軸光線の伝搬とFresnel-Kirchhoffの回折積分

いま，図2の様に光ビームがz軸近傍を伝搬しており，ある面\((x,y)\)上で強度および位相が決まっているとする．このとき，距離\(l\)離れた\((X-Y)\)面上の光電場は，以下の積分で求められる．

\begin{align} 　E(X,Y)=\frac{\exp(jkl)}{j\lambda l}\iint E(x,y)\exp\left[\frac{jk}{2l}\left\{(x-X)^2+(y-Y)^2\right\}\right]\rd x \rd y \end{align}

図3: Fox-Li型光共振器シミュレーションの概念

Fresnel-Kirchhoffの回折積分を基本原理とした光共振器の数値計算は以下のように行われる．まず，光共振器の2枚のミラーを，\(z\)軸上の2箇所に置く．そして，これらの面を図2における\((x-y)\)面と\((X-Y)\)面とする．\((x-y)\)面上に適当な電場分布を置き，\((X-Y)\)面に向かって伝搬させる．\((X-Y)\)面上では，ミラーが存在する範囲の電場が反射，\((x-y)\)面に向かって逆方向に伝搬し(一部は透過させても良い)，残りは捨てられる．1往復して\((x-y)\)面に到達した電場のうち，ミラーが存在しない範囲は捨てられ，残りは再び\((X-Y)\)面に向かって伝搬する．

これを何度も繰り返しているうちに，2枚のミラー間を往復する電場は一定の空間分布を持つようになる．これがこの2枚のミラーからなる光共振器の共振モードである．

図4: 実際に行われた計算の結果．
左：計算領域内部の電場分布．下の数値は往復回数　　右：計算領域内に存在する電磁場のパワー

図4は，実際に行われた計算の一例である．領域内を往復している電場分布ははじめはランダムだが，やがて一定のパターンを取り始め，何度かの変化を経て最終的には一つのモードに収束していく．

光電場が往復するたびに失われるパワーは，ミラー面上に仮想の利得媒質を置くことで補償され，上の計算も実際にそれを行っているが，ここでは詳しくは触れない．

現代でも，FoxとLiが提唱したこの手法に連なるシミュレーションは，「Fox-Li type」と呼ばれている．

　

光共振器の理論計算を行おうという動機を，その目的で分類すると以下の3つになる．

1. レーザーの性能向上を，試作することなく達成したい．
2. 現状では製作困難な大規模レーザーの性能を理論的に予測したい．
3. 現在直面している問題の原因を，理論的側面から解明したい．

本研究室では，上述の3つのカテゴリーに分類される様々な問題に直面し，その都度カスタムメイドの光共振器シミュレーションを作ってそれを解決してきた．以下では，そのうちの代表的なものについて紹介したい．

図5: 同軸円筒スラブCO₂レーザー

あるメーカーが開発中の，同軸円筒スラブCO₂レーザーの光共振器について相談を受けた． レーザーの構造概念図を図5に示す．レーザー媒質は炭酸ガスで，拡散冷却を促進するため薄い円筒形の容器に封入されている．単純な2枚の球面ミラーではドーナツ状のレーザービームになってしまうため，Waxiconで折り返して中実なビームを出力するように設計した．ところが，光共振器の発振モードが，2つのローブを持つTEM₀₁になってしまうのだと言う．問題解決のため，光共振器シミュレーションを組んでミラー形状を様々に変え，発振モード，出力を解析した．

問題の直接的な原因は，同軸円筒スラブの内側円筒を支える2本の柱であった．同軸スラブのレーザー媒質は，内側のスラブをリング状のサポートで支えて浮かせている．このとき，内側スラブを支えるサポートは光の通り道に露出する(図6)．

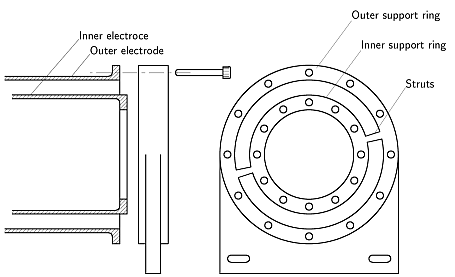
図6: 同軸スラブ型レーザー媒質のサポート構造

光共振器には基本モードの他に高次モードが存在するが，実際にレーザー媒質を詰め，発振させると最も損失の少ないモードが最初に発振する．殆どの場合，これは基本モード(TEM₀₀)なのだが，この光共振器は2本の柱がじゃまになり，TEM₀₁モードが発振する結果となっていた．柱がなければ良いのだが，設計上なかなか難しい．そこで，図5のToric mirrorの形状を工夫し，基本モードの損失が高次モードの損失より小さくなる方法を見出した．

図7: 同軸スラブ光共振器のミラー形状を変化させる

具体的な方法を説明するのが図7である．図5左端のリング状ミラーの曲面の底(vertex)の位置を変える．すると，共振器の1往復あたり損失が図8の様に変化する．

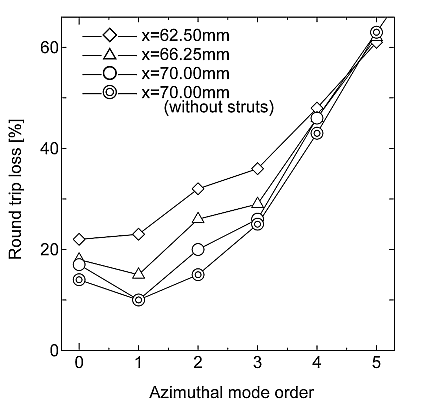
図8: 同軸スラブ光共振器の小信号損失を，vertexの位置をパラメータにして計算

Vertexの位置を62.5mmに設定することで，最低次モードの損失が最も小さくなる．その結果，光共振器はTEM₀₀モードで発振することになる．CO₂レーザー媒質を仮定したモデルで計算し，確認したところ図9の様な結果を得た．

図9: 同軸スラブ光共振器の発振モード

計算結果をまとめ，J. Phys. Dに投稿した．
M. Endo, S. Yamaguchi, T. Uchiyama, and T. Fujioka, “Numerical Simulation of the W-Axicon type Optical Resonator for Coaxial Slab CO₂ Lasers”, J. Phys. D 34, pp. 68-77, 2001.

  

2006年ころから，太陽光励起レーザーに興味を持ちはじめた．太陽光励起レーザーは，太陽光を励起光とするレーザーで，無尽蔵の太陽光から直接レーザーが得られる点が最大の特徴．その応用は主に得られたレーザー光を利用したエネルギー変換である．したがって太陽光励起レーザーは，大出力であることが前提で，そのため，レーザー媒質も大型となる．

ところが，大きなレーザー媒質から高品質なレーザー光を取り出すのは大変むずかしい．化学レーザーでさんざん経験したことが，太陽光レーザーのコミュニティでほとんど議論されていないことに不満を持ち，「太陽光励起レーザーで成立する，高品質なビームを生成する光共振器」のアイデアを提案した．

図10: Conical-toroidal型光共振器

光共振器の概念図を図10に示す．名付けて"Conical-toroidal optical resonator"である．レーザー媒質は薄い円盤状で，これが冷却装置に張り付く形で取り付けられる．一般に，こういうタイプの固体レーザーは"Active mirror"または"Thin disk"タイプとして知られているが，それらのレーザーと異なり，本研究で提案した概念では，共振モードは媒質を半径(ラジアル)方向に伝搬する．媒質はドーナツ状で，内側の穴には三角コーン状ミラーがあり，これがラジアル伝搬ビームを再びドーナツ状の近軸光線に変換する．

このアイデアの良い点は，太陽光の様に強集光が難しい励起光でも，媒質の広い面積で励起光を受けることができるため利用が可能である一方で，共振モードは回折限界に近いビーム品質が得られる点である．

ただし，シミュレーションは一筋縄ではいかない．ドーナツ状のレーザー媒質を半径方向に光伝搬するようFresnel-Kirchhoffの伝搬公式を変形し，更に，媒質内のスラブ導波路モードを模擬するため，折り返し伝搬計算法を開発した．これらの概念を図11，図12に示す．

図11: Conical-toroidal光共振器のシミュレーションの概念図

図12: 導波路モードを折り返しでモデル化するアイデアの概念

レーザー媒質にNd/Cr: GSGGを選定，直径21cm，厚さ2.5mmの，焼く前のピザくらいの大きさのレーザー媒質で，どの程度の出力が出せるかを計算した．結果を図13に示す．最大出力は約8kW，光-光変換効率は6%弱，という計算結果が得られた．これくらの出力なら，エネルギー応用としても充分期待できる．

図13: レーザー出力およびエネルギー変換効率の計算結果

レーザービームのパターンの計算結果を図14に示す．ビームパターンはTEM₀₁^*と呼ばれるドーナツ状のモードで，これは予想通りだったのだが，予想外のことは，ミラー表面のS偏光とP偏光のわずかな反射率の差で，発振モードがラジアル偏光，アジマス偏光に変化することであった．この計算の結果が，この後Triple-axiconミラーのアイデアにつながっていく．

図14: モードパターンの計算結果．左は強度分布，右は電場ベクトル分布．

計算結果をまとめ，Opt. Expressに投稿した．
M. Endo, “Feasibility study of a conical-toroidal mirror resonator for solar-pumped thin-disk lasers,” Opt. Express 15 (2007), pp. 5482-5493.

　

上述の，Conical-toroidal光共振器が図らずも軸対称偏光ビームを生成することが明らかになった．ハイパワーの軸対称偏光ビームはレーザー加工に有利と言われている．幾つかの方法が提案されているが，アクシコンを使った方法は未だなかった．そこで，上記のアイデアを発展させて，当時所持していたAmada製2kW級CO₂レーザーをラジアル偏光で発振させるミラーを考案した．それが，図15の"Triple-axicon retroreflector" (T-axicon)である．

図15: Triple-axicon retroreflectorの概念と偏光選択の原理

T-axiconが偏光を選択するメカニズムは上述のConical-toroidal光共振器と同じである．3つのアクシコンの組み合わせは，入射ビームを6回反射で来た方向と同じ方向に反射させる．このとき，S偏光とP偏光の僅かな反射率の差が，6回反射で増強され，光共振器のモード成長に決定的な差となって，光共振器はどちらかの反射率が高い方のモードで発振する．

アクシコンを3つ組み合わせた理由は，ミスアライメントに対する寛容性を高めるためだ．retrorefelctorとは，どの方向から入射しても同じ方向に光が反射する鏡で，有名なところではアポロ宇宙船が月に置いてきたミラー，卑近なところでは道路脇の反射板などが挙げられる．

図16: 二つの代表的なretroreflector．コーナーキューブミラーとキャッツアイ．

計算モデルは，Conical-toroidal光共振器の際に開発したものを少々改造するだけで事足りる．計算領域の概念図を図17に示す．

図17: Triple-axicon光共振器のシミュレーション．計算は，近軸伝搬領域(A，C)と放射状伝搬領域(B，D)の二つに分けられ，それらを中央のコーンが幾何学変換で接続している．

一連の計算の結果，単純な平面鏡からなるT-axiconは，回折損失が大きく，光共振器に組み込むには最適化設計が必要ということがわかった．詳細は省略するが，あるレーザー装置が条件として与えられたとき，最適なT-axiconの形状はそのレーザーの共振器長，放電領域の口径によって決まり，(R=50m程度の)緩やかな曲面とする必要があることがわかった．最適化設計の一例を図18，図19に示す．

図18: T-axiconの最適設計の一例．中央コーン高さ\(h\)，反射帯の幅\(W\)，表面の曲率\(R\)，そしてVertexの位置\(D_v\)がパラメータ．

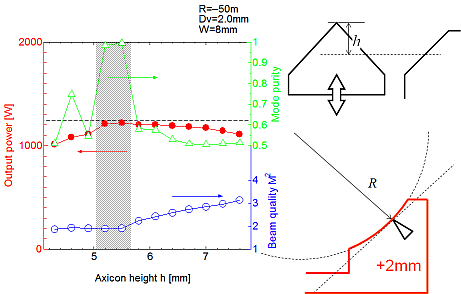
図19: 計算結果の一例．\(R=-50\)m，\(D_v=2.0\)mm，\(W=8.0\)mmを固定，\(h\)とレーザー出力，ビーム品質の関係を示す．

詳しい計算結果はSPIEの国際会議で報告した．

M. Endo, “Development of an optical resonator with conical retroreflector for generation of radially polarized optical beam,” Photonics West 08 Laser Resonators and Beam Control X (San Jose, CA), Jan. 2008, Proc. SPIE 6872 (2008), 687207 (10pp).

そして，計算を元にミラーを製作，Amada製レーザーに組み込んだ．結果は，「半分成功，半分失敗」だった．反射率はR_s<R_pになるように設計し，ラジアル偏光で発振することを目論んだのだが，結果はアジマス偏光で発振した．CO₂レーザーには9.6\(\mu\)mと10.6\(\mu\)mに利得があるのだが，先に9.6\(\mu\)mの方が発振してしまったためである．一般に，誘電体多層膜の反射率には鋭い波長依存性があり，今回特注した多層膜は9.6\(\mu\)mではR_s>R_pであったためこのような結果となった．しかし，世界初の成果だ．実験結果を早速Opt. Lett.に投稿した．

図20: T-axiconを組み込んだAmada OLC-H420．リア側ミラーを取り外し，T-axiconを組み込む以外の改造は加えていない．

M. Endo, “Azimuthally polarized 1 kW CO2 laser with a triple-axicon retroreflector optical resonator,” Opt. Lett. 33 (2008) pp. 1771-1773.

当時はまだ誘電体多層膜についての勉強が不足で，R_s<R_pになるような膜設計が大変困難であることに充分理解がなかった．その後は，素直R_s>R_pになる一般的な誘電体多層膜で，アジマス偏光で発振するT-axiconを開発した．ラジアル偏光は，出力ビームを偏光板ペアに通すことで簡単にラジアル偏光にできる．

図21: アジマス偏光をラジアル偏光に変換する偏光変換器

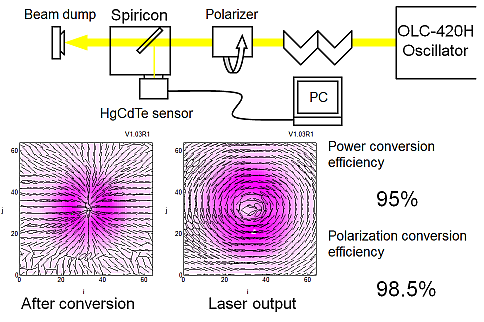
図22: 偏光計測の結果

結局，我々は，2kW級の出力を持つ，ラジアル・アジマス両偏光ビームを発生するCO₂レーザーを作り上げた．このレベルの出力で軸対称偏光のレーザービームを発生させる技術は，世界でもドイツIFSWのみであったから，この装置を使って行った加工実験は，数々の面白い結果を生み出した．詳しくは個々の研究成果を参照されたい．

M. Endo, “Sheet metal cutting with a 2 kW radially polarized CO2 laser,” XVIII International Symposium on Gas Flow and Chemical Lasers & High Power Lasers Conference (Sofia, Bulgaria), Sep. 2010, Proc. SPIE 7751 (2010), 77511B (9pp).
遠藤雅守, 「大出力軸対称偏光レーザ発生技術および加工応用」, レーザ加工学会誌 18 (2011), pp. 171-177. 　

　

図23: WWaxicon光共振器

これも，あるメーカーからの相談がきっかけで始めた研究．このメーカーでは，WWaxiconなる光共振器のレーザーを試作していた．概念図を図23に示す．どういう思想かというと，同社のレーザーは大きな口径のレーザー媒質を持つのが特徴で，それがゆえに基本モードで発振させるのに苦労していた．マルチパス共振器はアライメントが大変で，かつ媒質の体積を有効に利用できない．WWaxiconなら，レーザービームは利得体積を隙間なく通るので，発振効率が上がると考えた．ところが，これがまるっきり発振しない．理由もわからず困り果てていた．

シミュレーションを構築する上でのポイントは，現実の系を正しくモデル化しているという確証である．そこで，まずは既に発振している4パス共振器をモデル化，計算を行った．光共振器の概念図を図24に，計算結果を図25に示す．

図24: 4パス光共振器の計算モデル．4枚のミラーを1つの計算領域にまとめて記述する．

図25: 4パス光共振器の計算結果
左：M1面上の光電場強度分布　右：左のパターンをフーリエ変換したもの．ビームが進む方向を表す．

左はミラー面上のビームパタンーを2次元等高線で示したもの．左上のミラー以外は縞々になっているが，これは，ミラーが面に対して傾いているためだ．4パス共振器は，反射光を入射光と異なる方向に反射させる必要から，ミラーは互いに異なる角度で固定されている．こういった場合，計算は，ビームが通るパスにそって\(z\)軸を設定するのだが，私はこれでは問題を解明することはできないと考えた．そこで，4枚のミラーが同時に入る，大きな計算格子を用意した．2000年代初頭の計算機パワーではとても実行できなかっただろう．

右は，左のパターンをフーリエ変換したもので，ビームがどちらの方向に，どれくらいの角度で飛んで行くかがわかる．結果は，光共振器を進むビームの角度に一致した．

続いて，WWaxicon光共振器でおなじ計算を行った．すると，結果は，奇妙なパターンを呈する，ほとんど出力が得られないモードとなった．結果を図26に示す．同様に，左がM1上パターン，右がそれをフーリエ変換したものだ．この結果から，レーザーは，「出力がほとんど外に出ていかない」モードで発振していたことがわかった．設計上の光伝搬経路と，実際の光伝播経路を図27に示す．

図26: WWaxion光共振器の計算結果．右のパターンから，光パワーが内部に閉じ込められてほとんど外に出ていかないことがわかる．

図27: WWaxiconの，設計上想定されたビーム伝搬経路(上)と，実際のビーム伝搬経路(下)．

これを防ぐ方法は簡単で，内周と外周をまたぐ，斜め伝搬を禁止するリングを共振器内に置けばよい．リングの概念を図28に示す．右は，シミュレーション計算の結果得られた，リングの長さの関数で表したレーザー出力およびビーム品質を示している．ここから，リングの長さは400mmほど必要とわかる．また，レーザー出力はマルチパスの2倍以上が期待できることもわかる．

　　　　　
図28: 左：斜め伝搬モードを防ぐための仕切り　右：仕切りの長さとレーザー出力，ビーム品質の関係

長さ40cmのリングを装着したレーザーの発振モードを図29に示す．今度は，レーザーは設計意図どおりのモードで発振した．

図29: 設計意図どおりのモードで発振したWWaxicon光共振器の内部強度

計算結果をまとめ，J. Opt. Soc. Am. Aに投稿した．
M. Endo, M Sasaki, and R. Koseki, “Analysis of an optical resonator formed by a pair of specially shaped axicons,” J. Opt. Soc. Am. A 29 (2012), pp. 507-512.

　

図30: 東海大のDPAL装置の利得セル．上：外観　下：内部の様子

東海大で開発したDPALの利得媒質セルを図30に示す，DPALは，気体状のアルカリ金属に半導体レーザーのポンプ光を同軸で照射してレーザー媒質を生成する．したがって，レーザーの性能には，ポンプ光の空間分布，レーザーモードとポンプ光の空間的な重なりが大きな影響を与える．

これまで，アルカリレーザーの性能を予測するシミュレーションが数多く発表されてきたが，それらはいずれも上述のポンプ光とレーザーモードのカップリングを正確にモデル化したものではない．理由は，光ビームの伝搬にはFresnel-Kirchhoffの伝搬公式を利用したFox-Liタイプのシミュレーションを実行する必要があるが，これがレーザー媒質の生成をモデル化するレート方程式と相性が悪く，両者を結合したシミュレーションを構築することが困難だったことによる．

図31: 波動光学モデルを採用したDPALシミュレーションの概念図

私はこの課題に果敢に挑み，一定の成果を得た．モデルの概念図を図31に示す．モデルは，今までに開発してきた光共振器のコードをベースにして，利得を記述するunit cellにDPALのレート方程式を組み合わせたものである．また，伝搬するポンプ光も同様にFresnel-Kirchhoffの回折積分で記述，その空間分布を正確に再現した点もポイント．実際に計測したポンプ光の空間分布と，シミュレーションで再現したポンプ光の空間分布の比較を図32に示す．詳しい説明は省くが，ビーム品質が悪いマルチエミッターの半導体レーザーの伝搬をFresnel-Kirchhoffの回折積分で再現するのは難しく，計算上の工夫が凝らされている．

図32: ポンプ光ビーム伝搬のモデルと，実測されたポンプ光の軌跡を比較．

各unit cellでは光子レート方程式と原子レート方程式を連成して，局所的な利得を計算，それを光共振器コードに送っている．

図33: 各unit cellで行われれているレート方程式の計算と，光共振器コードとの連成

この研究は，既に立派に動くDPAL装置があるので，「どれだけ実験結果と近い計算結果が得られるか」がシミュレーションの価値を決める．そこで，実験装置を様々な動作条件で動かし，同じ条件の計算を行って結果を比較した．一例を図34に示す．

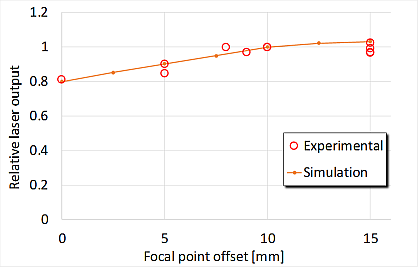
図34: 実験結果と計算結果の比較(1)．集光レンズ位置とレーザー出力の関係

この計算は，半導体レーザーを集光するレンズの焦点位置を変え，レーザー出力を求めたものである．半導体レーザーはビーム品質が悪いため，焦点近傍以外では大きく広がる．したがってセル内の空間分布は焦点の位置を変えると大きく変わり，結果としてレーザー出力も変わる．結果は図35の様に，実験結果と計算結果はピタリと一致した．

更に，我々は実験において，レーザー媒質の密度を増やしていくと，ある程度以上から先はレーザー出力が増加せず，むしろ減少するという現象を観測していた．これはDPALの出力roll overと言われる現象で，その解明が待たれていた．

図35: 実験結果と計算結果の比較(2)．レーザー媒質温度とレーザー出力の関係．

我々はシミュレーションを行い，実験結果を再現することに成功した．こうなると，roll overを引き起こした物理現象が何なのか，解明することは容易である．シミュレーションで起こっていることは全て計算機内で起こっていることなので，どんな物理量でも，いくらでも詳細に知ることができる．調査の結果，レーザー媒質の濃度が高くなっていくと，アルカリ原子のD₁線の自然放出光強度がレーザー出力に匹敵するほど大きくなり，これが反転分布形成を阻害していることが明らかとなった．

図36: シミュレーションから明らかになった，過程別に分別した吸収ポンプ光パワーの損失

結果をまとめ，SPIEの国際会議で発表した．
M. Endo, R. Nagaoka, H. Nagaoka, T. Nagai and F. Wani, “Wave optics simulation of diode pumped alkali laser (DPAL),” Photonics West 16 High Energy/Average Power Lasers and Intense Beam Applications IX (San Francisco, CA), Feb. 2016, Proc. SPIE 9279 (2016), 927906 (10pp).